Alberta’s Fiscal Responses To Fluctuations In Non-Renewable-Resource Revenue

Introduction

This is my replication of the empirical results, tables, and figures produced in a paper by Dr. Ergete Ferede, published by the University of Calgary school of public policy in Volume 11:24, September 2018.

The original paper is here: https://www.policyschool.ca/wp-content/uploads/2018/09/NRR-Ferede.pdf

I chose this paper to reproduce for two reasons. The first is pragmatic; the data it uses is all publicly available, so I actually can. The second is that it describes a topic of importance in the province of Alberta, where I live.

You can read the details of what the paper sets out to show in the paper itself, but in brief the idea is to show that provincial government spending increases in the year following an increase in non-renewable resource revenue, but it does not decrease accordingly in the year following declines in the same revenue source. This has a ratcheting effect on public finance that is a contributor to the “royalty rollercoaster” that is Alberta’s public finance.

In the following sections I’ll go through the code necessary to extract and transform the data set used in the paper, as well as reproduce its key empirical results. Since most economists don’t use python, and they make up a key part of my intended audience for this, I’ll be adding comments to my code that explicitly describe what some of the functions and methods I’m calling do.

I’m including all of the code necessary to produce this reproduction, since that’s a big part of why I’m doing this exercise, but if you’re just interested in seeing how my reproduced results compare to the original paper you can skip all the code blocks. You can find the code for this notebook on my github

A surprising result of this reproduction is that I’ve identified a single data point error in the original paper that negates its results. Read on to find out what the error was and the impact it had on the results.

Setup and data acquisition

This section of the code loads required modules, downloads the required data sets, and reads them into DataFrames.

import datetime as dt
from itertools import chain
from pathlib import Path

import altair as alt
from arch.unitroot import DFGLS, ADF, PhillipsPerron
from IPython.display import Image
import pandas as pd
import pandas_datareader as pdr
import requests
import seaborn as sns
import stats_can
import statsmodels
from statsmodels.tsa.api import VAR


%matplotlib inline
alt.renderers.enable("jupyterlab");

We start by loading the required libraries that will be used to support the analysis. For reference here are links to the libraries that are being used:

• Pathlib
• datetime
• requests
• pandas
• pandas_datareader
• numpy
• stats_can
• altair
• seaborn
• arch
• statsmodels
• matplotlib

Historical budget data

Functions in this section are concerned with acquiring historical Alberta budget data and reading it into a DataFrame

def download_budget_data() -> Path:
    """Download the excel file for the analysis from the policy school page.

    Note the readme sheet on the first file. Credit to Kneebone and Wilkins for
    assembling it, and policy school for hosting it.

    Originally used this URL, but found it was missing some later heritage
    contributions. After discussion with Dr. Kneebone an updated set has been provided
    https://www.policyschool.ca/wp-content/uploads/2019/01/Provincial-Government-Budget-Data-January-2019FINAL-USE.xlsx

    Returns
    -------
    pathlib.Path
        A path object with the location and name of the data
    """
    print('Downloading data set')

    url = 'https://www.policyschool.ca/wp-content/uploads/2019/03/Provincial-Government-Budget-Data-March-2019.xlsx'
    # send a request to the url for the file
    response = requests.get(
        url,
        stream=True,
        headers={'user-agent': None}
    )
    # create a path object for the file in the data folder above
    # where this notebook is saved with the file named
    # budget.xlsx for easy later access.
    fname = Path('.').joinpath('data').joinpath('budgets.xlsx')
    # write the response from the request to the file in the path specified above
    with open (fname, 'wb') as outfile:
        for chunk in response.iter_content(chunk_size=512):
            if chunk: # filter out keep-alive new chunks
                outfile.write(chunk)
    # Return the location of the file so we can load it later easily
    return fname


def get_budget_file(force_update: bool=False) -> Path:
    """Get the budget file, downloading if required.

    Parameters
    ----------
    force_update: bool
        Download the data file even if you already have it

    Returns
    -------
    pathlib.Path
        A path object with the location and name of the data
    """
    # This is where we're expecting the file to be saved if it exists
    fname = Path('.').joinpath('data').joinpath('budgets.xlsx')
    if not fname.exists() or force_update:
        download_budget_data()
    return fname


def get_date_index(df: pd.DataFrame) -> pd.DatetimeIndex:
    """Helper function to turn budget year strings into datetimes.

    The Fiscal year columns span across years, e.g. 1965-66. In order
    to use all the date indexed functionality I want to convert them into
    an actual datetime format. This function accomplishes that
    
    Parameters
    ----------
    df: pd.DataFrame
        The budget dataframe with the fiscal year style columns
    
    Returns
    -------
    pd.DatetimeIndex
        A datetime index showing January 1 of the beginning of each
        fiscal year for each period.    
    """
    date_index = pd.to_datetime(
        df
        .assign(year=lambda df: df['budget_yr'].str[0:4].astype(int))
        .assign(month=1)
        .assign(day=1)
        [['year', 'month', 'day']]
    )
    return date_index


def read_ab_budget() -> pd.DataFrame:
    """Read Alberta budget data.

    Downloads the data if necessary, reads it in and gives
    the variables easier to work with names

    Returns
    -------
    pd.DataFrame
        Alberta's revenue and expenditure tables
    """
    # Get the budget file, download if necessary  using functions
    # defined above
    fname = get_budget_file()
    df = (
        pd.read_excel(
            fname,
            sheet_name='Alberta',
            # column titles are spaced over 3 rows
            header=3,
            # first column of data is B
            index_col=1,
            # there's a big footnote at the bottom we want to skip
            skipfooter=21
        )
        # Because of the merged cells we get an empty first row
        .loc[lambda x: x.index.notnull()]
        # Not sure where the empty first column comes from but drop it
        .drop(columns='Unnamed: 0')
        .reset_index()
        .rename(columns={
            'index': 'budget_yr',
            'Personal Income Tax': 'personal_income_tax',
            'Corporation Income Tax': 'corporate_income_tax',
            'Retail Sales Tax': 'retail_sales_tax',
            'Federal Cash Transfers': 'federal_cash_transfers',
            'Natural Resource Revenue': 'natural_resource_revenue',
            'Other Own-Source Revenue': 'other_own_source_revenue',
            'Total Revenue': 'total_revenue',
            'Health': 'health_exp',
            'Social Services': 'social_services_exp',
            'Education': 'education_exp',
            'Other Program Expenditures': 'other_program_exp',
            'Total Program Expenditures': 'total_prog_exp',
            'Debt Service': 'debt_service',
            'Total  Expenditures': 'total_exp',
            'Unnamed: 16': 'annual_deficit'
        })
        # Turn the fiscal year string into a datetime object
        .assign(budget_dt=lambda df: get_date_index(df))
        .set_index('budget_dt')
    )
    return df


def read_heritage() -> pd.DataFrame:
    """Read deposits to the heritage trust fund from a separate table.

    The paper nets out contributions to the heritage trust fund when they are
    made, so we have to read them in to be able to net them out of resource revenue.

    They're stored in the same sheet of the workbook, just down below the big table we
    read in with the function above.
    """
    fname = get_budget_file()
    df = (
        pd.read_excel(
            fname,
            sheet_name='Alberta',
            # Have to manually specify column names because of
            # how the table is laid out
            header=None,
            usecols='D:G',
            names=['budget_yr', 'resource_allocation', 'deposits', 'advance_edu'],
            skiprows=71,
            skipfooter=1
        )
        # more fiddly cleaning because of how the table is set up
        # there's a blank row between 1986-87 and when
        # contributions resume in 2005-06
        .loc[lambda df: ~df['budget_yr'].isna()]
        .set_index('budget_yr')
        # missing entries have 0 contributions for that
        # category in that year
        .fillna(0)
        # The three columns are all counted the same
        # for the purposes of this analysis, they just have
        # different labels/classifications depending on the year
        .assign(total_heritage=lambda df: df.sum(axis='columns'))
        # Add a dummy variable to indicate heritage fund deposit years
        .assign(heritage_dummy=1)
        .reset_index()
        # convert the fiscal year column to a datetime index
        .assign(budget_dt=lambda df: get_date_index(df))
        .drop(columns='budget_yr')
        .set_index('budget_dt')
    )
    return df


def clean_budget() -> pd.DataFrame:
    """Combine base budget with heritage deposits.

    Pull all the logic together to create one dataframe with all the
    fiscal data for the period of interest.

    Returns
    -------
    pd.DataFrame
        The full nominal budget data set.
    """
    budg = read_ab_budget()
    heritage = read_heritage()
    budg_clean = (
        # Start with the budget dataframe
        budg
        # consolidate some revenue categories
        .assign(other_revenue=lambda df: df[['retail_sales_tax', 'federal_cash_transfers', 'other_own_source_revenue']].sum(axis='columns'))
        # Just keep the columns we still need
        .reindex(columns=['personal_income_tax', 'corporate_income_tax', 'natural_resource_revenue', 'other_revenue', 'total_prog_exp', 'debt_service'])
        # add in the heritage contributions data
        .merge(heritage[['total_heritage', 'heritage_dummy']], how='left', left_index=True, right_index=True)
        # Set contributions and the heritage dummy to 0 for years where there were no contributions
        .fillna(0)
        # Net out heritage contributions from natural resources revenue
        .assign(natural_resource_revenue_before_heritage=lambda df: df['natural_resource_revenue'])
        .assign(natural_resource_revenue=lambda df: df['natural_resource_revenue'] - df['total_heritage'])
        # consolidate revenue
        .assign(total_revenue=lambda df: df[['personal_income_tax', 'corporate_income_tax', 'natural_resource_revenue', 'other_revenue']].sum(axis='columns'))
        # consolidate expenditure
        .assign(total_expenditure=lambda df: df[['total_prog_exp', 'debt_service']].sum(axis='columns'))
        # calculate the deficit
        .assign(deficit=lambda df: df['total_expenditure'] - df['total_revenue'])
        # make all the budget numbers floating point
        .astype('float64')
    )
    return budg_clean

Real Per Capita budget

All of the analysis in the paper is done in terms of real per-capita data. Functions in this section transform the nominal total budget numbers acquired in the previous section into real per-capita figures.

def periodic_to_budget_annual(df: pd.DataFrame, index_name: str, year_periods: int = 4) -> pd.DataFrame:
    """Take a monthly or quarterly indexed dataframe and annualize it by budget period.

    The inflation and population data we need to convert the budget into
    real per-capita figures are monthly series. We need to get the average
    population and price level for each fiscal year in the data set.

    Rolling mean indexed on January year N+1 is the March to March
    average population for fiscal year N
    Applying a date offset of -1 year and taking only
    January data of these rolling means gives us an average on the
    same basis as the budget dates.

    Parameters
    ----------
    df: pandas.DataFrame
        DataFrame to be piped into this function
    index_name: str
        The name of the date index
    year_periods: int, default 4
        4 for quarterly data (population), 12 for monthly (inflation)

    Returns
    -------
    pd.DataFrame
        An annualized dataframe on a fiscal year basis for comparison
        to annual budget figures.
    """
    df = (
        df
        .copy()
        .rolling(year_periods, closed='left')
        .mean()
        .reset_index()
        .assign(budget_dt=lambda df: df[index_name] - pd.DateOffset(years=1))
        .loc[lambda x: x['budget_dt'].dt.year >= 1965]
        .loc[lambda x: x['budget_dt'].dt.month == 1]
        .drop(columns=index_name)
        .set_index('budget_dt')
        .copy()
    )
    return df


def per_capita_data() -> pd.DataFrame:
    """Read in population data to calculate per capita estimates.

    Quarterly population estimates for Alberta from Statistics Canada

    Returns
    -------
    pd.DataFrame
        Fiscal year annualized population estimates for Alberta over the
        reference period.
    """
    table = '17-10-0009-01'
    df = (
        stats_can.table_to_df(table, path='data')
        .loc[lambda x: x['GEO'] == 'Alberta']
        .loc[lambda x: x['REF_DATE'] >= '1965']
        .set_index('REF_DATE')
        [['VALUE']]
        .rename(columns={'VALUE' : 'population'})
        .pipe(periodic_to_budget_annual, 'REF_DATE', 4)
    )
    return df


def inflation_data() -> pd.DataFrame:
    """Read in inflation data to calculate real dollar estimates.

    The whole series is scaled so 2017 budget year is = 1

    Returns
    -------
    pd.DataFrame
        Fiscal year annualized inflation data for Alberta over
        the reference period. Normalized to 2017 = 1
    """
    # Alberta inflation doesn't go back far enough, use Canada for earlier dates
    vecs = ('v41692327', 'v41690973')
    df = (
        stats_can.vectors_to_df_local(vecs, path='data', start_date=dt.date(1965, 1, 1))
        .rename(columns={'v41692327': 'ab_inflation', 'v41690973': 'ca_inflation'})
    )
    # fill in with Canadian inflation data where (early) Alberta inflation data is missing.
    mask = df['ab_inflation'].isna()
    # Could probably do some interpolation or scaling before this, but I looked
    # at the raw series and they were pretty comparable
    df.loc[mask, 'ab_inflation'] = df.loc[mask, 'ca_inflation']
    df = (
        df
        .drop(columns='ca_inflation')
        .pipe(periodic_to_budget_annual, 'REF_DATE', 12)
    )
    # Rescale to 2017 = 100 (this is fiscal year 2017,
    # original may have done calendar year)
    inf_2017 = float(df.loc['2017', 'ab_inflation'])
    df = df / inf_2017
    return df


def budget_real_per_capita() -> pd.DataFrame:
    """Get budget data in real per-capita terms.

    Returns
    -------
    pd.DataFrame
        Budget data in real per-capita terms.
    """
    # Read in budget data using the function defined in the 
    # previous section
    clean_budget_df = clean_budget()
    # Everything except the dummy variable gets turned into
    # real per-capita terms
    scale_cols = clean_budget_df.columns.drop('heritage_dummy').tolist()
    # Get population
    per_capita = per_capita_data()
    # Get inflation
    inflation = inflation_data()
    # Combine the datasets, can just use assign because they all
    # have a datetime index
    dfpc = (
        clean_budget_df
        .assign(pop=per_capita)
        .assign(cpi=inflation)
    )
    # rescale to real per capita
    dfpc[scale_cols] = (
        dfpc[scale_cols]
        # original data was in millions of dollars
        .mul(1_000_000)
        # divide by population and inflation for
        # real per-capita
        .div(dfpc['pop'], axis='index')
        .div(dfpc['cpi'], axis='index')
    )
    return dfpc

Exogenous factors

The paper lists the Alberta employment rate, the Alberta unemployment rate, and the CAD/USD exchange rate as exogenous factors included in the model. Functions in this section acquire that data. I had to do some fiddling to get long enough historical series for some of the factors as you’ll note in the code. It’s hard to say for sure how the original author sourced this data. I’ll just have to compare my tables and charts to his to see if I got close enough.

def download_historical_cad_usd() -> pd.DataFrame:
    """Get exchange rates from before 1971.

    FRED live data only goes back to 1971, I need a longer series
    This was what I could find. It's annual only, so I can't do it on a budget
    year basis, but hopefully it will be close enough

    This whole function is just some gross munging to read in a table from a web page.
    Once it's called we save it to the data folder so I don't have to re-call it every
    time I run this notebook.
    """
    url = 'https://fxtop.com/en/historical-exchange-rates.php?YA=1&C1=USD&C2=CAD&A=1&YYYY1=1953&MM1=01&DD1=01&YYYY2=2019&MM2=04&DD2=01&LANG=en'
    df = pd.read_html(url)[29]
    headers = df.iloc[0]
    new_df  = (
        pd.DataFrame(df.values[1:], columns=headers)
        .rename(columns={'Year': 'year', 'Average USD/CAD': 'EXCAUS'})
        .assign(month=1)
        .assign(day=1)
        .assign(budget_dt=lambda df: pd.to_datetime(df[['year', 'month', 'day']]))
        .set_index('budget_dt')
        .reindex(columns=['EXCAUS'])
    )
    new_df.to_csv('./data/early_cad_usd.csv')
    return new_df


def read_historical_cad_usd(force_update: bool = False) -> pd.DataFrame:
    """Get exchange rates before 1971.

    This wraps the above function to read in the downloaded data
    if it's available and download and then read it if required.

    Parameters
    ----------
    force_update: bool
        Download the data set even if you already have it

    Returns
    -------
    pd.DataFrame
        Exchange rates from 1965 to 1971
    """
    fname = Path('.').joinpath('data').joinpath('early_cad_usd.csv')
    if not fname.exists() or force_update:
        return download_historical_cad_usd()
    else:
        return pd.read_csv(fname).set_index('budget_dt')


def download_cad_usd() -> pd.DataFrame:
    """Download monthly exchange data from FRED.

    For most of the period of interest I can get monthly
    data from FRED, so I'll do that where possible.

    Returns
    -------
    pd.DataFrame
        Most of the CAD/USD exchange data I need for this analysis.
    """
    df = pdr.get_data_fred('EXCAUS', start=dt.date(1970, 1, 1))
    df.to_csv('./data/cad_usd.csv')
    return df


def read_cad_usd(force_update=False):
    """Get monthly exchange data from FRED.

    This wraps the above function to read in the downloaded data
    if it's available and download and then read it if required.

    Parameters
    ----------
    force_update: bool
        Download the data set even if you already have it

    Returns
    -------
    pd.DataFrame
        Exchange rate data
    """
    fname = Path('.').joinpath('data').joinpath('cad_usd.csv')
    if not fname.exists() or force_update:
        return download_cad_usd()
    else:
        return pd.read_csv(fname, parse_dates=['DATE']).set_index('DATE')


def annual_cad_usd() -> pd.DataFrame:
    """Full series of CAD/USD in fiscal year format.

    Get FRED data and turn the monthly values into annualized on a budget
    basis for as much as possible. Fill in the remainder with calendar annual
    data from fxtop

    Returns
    -------
    pd.DataFrame
        Exchange data on an annualized basis.
    """
    # Create a datetime index of all the points we need
    annual_date_range = pd.date_range('1964-01-01', '2018-01-01', freq='AS', name='budget_dt')
    # Get the old annual stuff to fill in later
    old_df = read_historical_cad_usd()
    df = (
        # get the monthly series
        read_cad_usd()
        # annualize it
        .pipe(periodic_to_budget_annual, 'DATE', 12)
        # add in all the missing dates we need
        .reindex(annual_date_range)
        # fill those missing dates from the old annual data set.
        .fillna(old_df)
    )
    return df


def stats_can_exog() -> pd.DataFrame:
    """Bring in exogenous StatsCan data. Employment and Unemployment rates.

    Returns
    -------
    pd.DataFrame
        Exogenous data required from StatsCan
    """
    # Vectors for monthly series where available
    ur_vec = "v2064516"
    er_vec = "v2064518"
    annual_date_range = pd.date_range('1964-01-01', '2018-01-01', freq='AS', name='budget_dt')
    # for the earlier periods we only have annual data
    old_df = (
        stats_can.table_to_df('36-10-0345-01', path='data')
        # Get Alberta data only
        .loc[lambda x: x['GEO'] == 'Alberta']
        # Keep only the categories we care about
        .loc[lambda x: x['Economic indicators'].isin(['Population', 'Total employment', 'Unemployment rate'])]
        # pivot so the year is the row and the variables are the columns
        .pivot_table(index='REF_DATE', columns='Economic indicators', values='VALUE')
        .rename(columns={'Unemployment rate': 'unemployment_rate'})
        # calculate the employment rate
        .assign(employment_rate=lambda x: (x['Total employment'] / x['Population']) * 100)
        # drop the population, just used for calculating employment rate
        .reindex(columns=['unemployment_rate', 'employment_rate'])
        .rename_axis('budget_dt', axis='index')
        .rename_axis(None, axis='columns')
    )
    # Get monthly data where available
    df = (
        stats_can.vectors_to_df_local([ur_vec, er_vec], path='data', start_date=dt.date(1964, 1, 1))
        .rename(columns={ur_vec: 'unemployment_rate', er_vec: 'employment_rate'})
        # annualize
        .pipe(periodic_to_budget_annual, 'REF_DATE', 12)
        # get the full range of data we want
        .reindex(annual_date_range)
        # fill in the gaps with the old annual series
        .fillna(old_df)
        # Not ideal but even the annual series doesn't go quite back
        # far enough so we have to backfill the earliest available
        # data point
        .fillna(method='bfill')
    )
    return df


def exogenous_variables() -> pd.DataFrame:
    """Bring in exogenous parameters together.

    From the paper:
    We also include other exogenous variables that are likely to affect
    the province’s budget. It is known that the various components of the
    provincial budget can be influenced by the business cycle. Thus, following
    Buettner and Wildsain (2006), we account for the potential effects of the
    business cycle by including one-period lagged changes in the provincial
    employment and unemployment rates. Another important exogenous factor
    that is often cited in provincial budget documents as being important in
    influencing the provincial government’s oil royalty revenue is the Canadian-U.S.
    dollar exchange rate. For this reason, we control for this factor by
    including one period lagged changes in the Canadian-U.S. dollar exchange rate

    Returns
    -------
    pd.DataFrame
        All the necessary exogenous factors for reproducing the paper.
    """
    cadusd = annual_cad_usd()
    ur_er = stats_can_exog()
    df = pd.concat([cadusd, ur_er], axis='columns')
    return df

Exploratory Figures

Figure 1

Page 5 of the report charts Non-renewable Resource Revenue, Total Expenditure, and Total Revenue. All are in per-capita 2017 dollars. Reproducing this chart will be a good starting check that my data extraction and transformation matches the original author’s strategy.

def fig1(df: pd.DataFrame) -> alt.Chart:
    """Reproduce Figure 1 from the paper.

    Parameters
    ----------
    df: pd.DataFrame
        A dataframe with non-renewable resource revenue, total expenditure, and total revenue time series
    """
    chart_df = (
        df
        .loc['1970':'2016', ['natural_resource_revenue', 'total_revenue', 'total_expenditure']]
        .rename(columns={
            'natural_resource_revenue': 'Non-renewable Resource Revenue',
            'total_revenue': 'Total Revenue',
            'total_expenditure': 'Total Expenditure'
        })
        .reset_index()
        .melt(id_vars='budget_dt')
    )
    c_domain = ["Non-renewable Resource Revenue", "Total Expenditure", "Total Revenue"]
    c_range = ["green", "red", "blue"]
    chart = (
        alt.Chart(chart_df)
        .mark_line()
        .encode(
            x=alt.X('budget_dt:T', axis=alt.Axis(title=None)),
            y=alt.Y('value:Q', axis=alt.Axis(title='Per capita in 2017 dollars'), scale=alt.Scale(domain=(0, 14_000))),
            color=alt.Color('variable:N', legend=alt.Legend(title=None, orient='bottom'), scale=alt.Scale(domain=c_domain, range=c_range))
        )
        .properties(width=1250, height=500)
    )
    return chart

Here’s the original chart from the paper:

Image(filename="img/ferede_fig_1.png")

And here’s mine:

df = budget_real_per_capita()
fig1(df)

This graph looks very similar to the chart in the paper, with a notable exception of the 1976/1977 budget year. My chart shows Non-renewable Resource Revenue as slightly negative, whereas the original chart has it largely in line with 1975/1976 and 1977/1978. NRR is negative in my chart because I have netted out contributions to the Alberta Heritage Savings Trust Fund (AHSTF). To the best of my understanding, the original paper does the same, and the consistent values between the two in all other years supports that. Quoting the original paper:

The part of resource revenue that is saved in the AHSTF is not expected to influence the provincial government’s spending and revenue-raising choices. For this reason, in our analysis, we exclude the part of the resource revenue that is saved in the AHSTF from the non-renewable-resource revenue data.

For comparison, here is the same chart, but without netting AHSTF contributions from revenue:

no_net_df = (
    df
    .assign(total_revenue=lambda df: df["total_revenue"] + df["total_heritage"])
    .assign(natural_resource_revenue=lambda df: df["natural_resource_revenue"] + df["total_heritage"])
    .assign(deficit=lambda df: df["total_expenditure"] - df["total_revenue"])
)
fig1(no_net_df)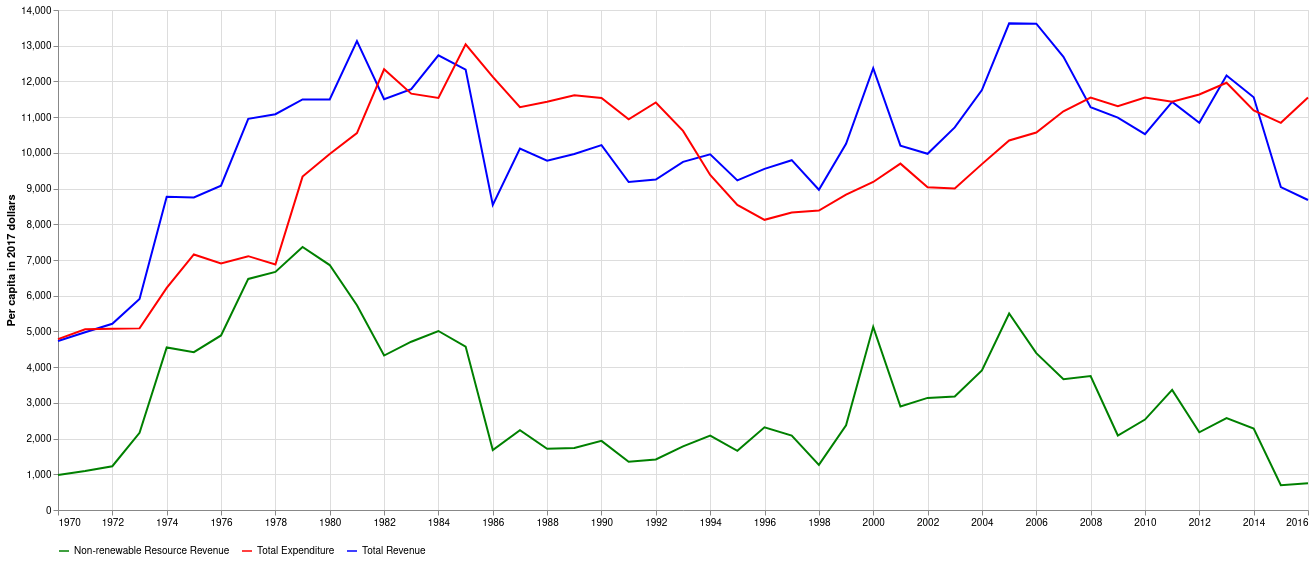

1976/1977 more closely matches the original chart in the paper, but the remaining years in the period of mid 70s to mid 80s when there were significant contributions clearly do not match. Let’s try one more where I just substitute that one year.

error_df = df.copy()
heritage_76 = error_df.loc["1976", "total_heritage"]
error_df.loc["1976", "natural_resource_revenue"] += heritage_76
error_df.loc["1976", "total_revenue"] += heritage_76
error_df.loc["1976", "deficit"] -= heritage_76
fig1(error_df)

Here’s the original figure again for easier comparison

Image(filename="img/ferede_fig_1.png")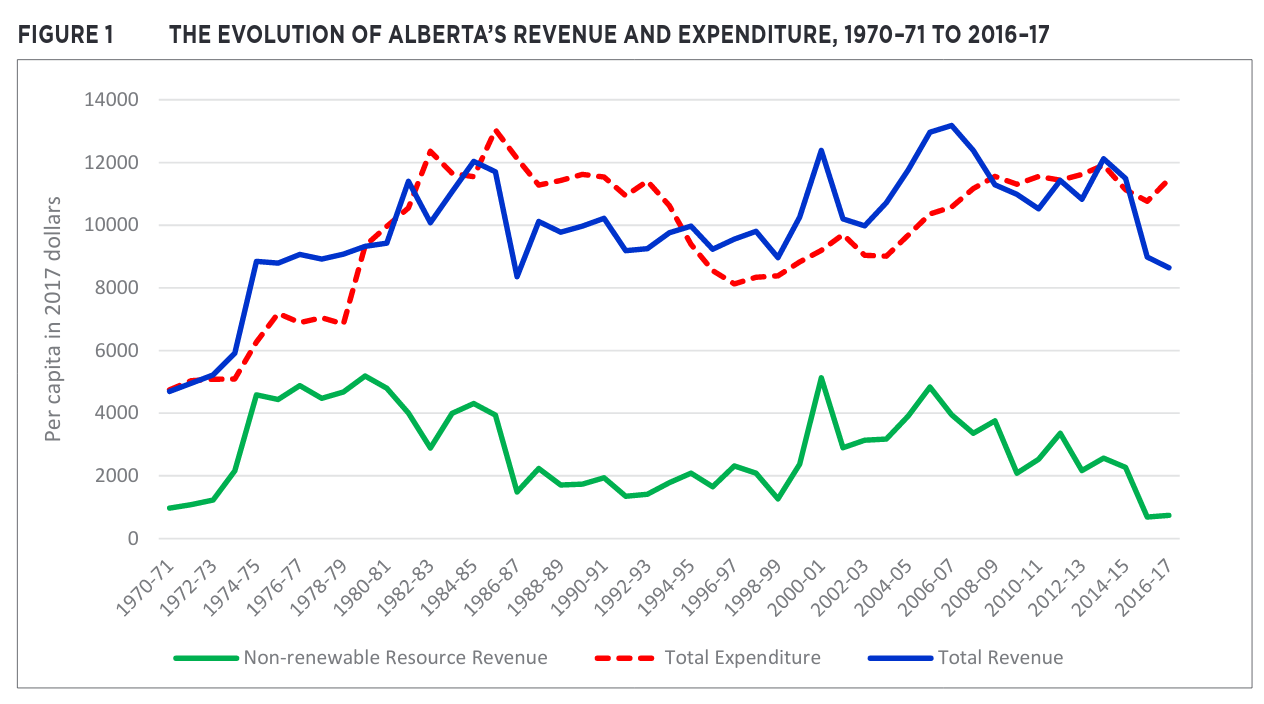

From eyeballing it that looks exactly like Figure 1 in the paper. It appears there’s a data error in the original paper. For the rest of this analysis I’ll compare both my base implementation of the data, as well as the one with the data error.

Figure 2

Page 6 of the paper produces a scatter plot of Real per capita non-renewable resource revenue on the X axis vs. Real per capita budget balance on the Y, along with a linear trend fit.

def fig2(df: pd.DataFrame) -> None:
    """Reproduce Figure 2 from the paper.
    
    Parameters
    ----------
    df: pd.DataFrame
        The table with historical revenue and expenditure data.
    """
    sns.set(rc={'figure.figsize':(11.7,8.27)})
    chart_df = (
        df
        .loc['1970':'2016', ['natural_resource_revenue', 'deficit']]
        .rename(columns={
            'natural_resource_revenue': 'Non-renewable Resource Revenue',
            'deficit': 'Deficit'
        })
        .assign(balance=lambda df: df['Deficit'] * -1)
        .rename(columns={'balance': 'Budget Balance'})
        .copy()
    )
    sns.regplot(x='Non-renewable Resource Revenue', y='Budget Balance', data=chart_df)

Here’s the original figure

Image(filename="img/ferede_fig_2.png")

Here’s the figure using my original data:

fig2(df)

And here’s the figure using the version with a data error:

fig2(error_df)

Again, this chart is more consistent with the dataframe where I don’t net heritage fund contributions out of 1976 but do for all other years

Model Specification and estimation

This section combines the previously specified data extraction with transformations necessary to produce summary statistics, statistical tests, and the VAR model itself.

def model_df_levels(budg: pd.DataFrame) -> pd.DataFrame:
    """Combine real per capita budget data to get model data in levels.

    lag exogenous variables (unemployment and employment rates, CAD/USD exchange)

    Parameters
    ----------
    budg: pd.DataFrame
        Budget data, either with or without data error

    Returns
    -------
    pd.DataFrame
        Budget data combined with exogenous factors
    """
    exog = exogenous_variables()
    df = (
        pd.concat([budg, exog], axis='columns')
        .rename(columns={'total_prog_exp': 'program_expenditure', 'EXCAUS': 'cad_usd'})
        .assign(ur_lag=lambda df: df['unemployment_rate'].shift(periods=1))
        .assign(er_lag=lambda df: df['employment_rate'].shift(periods=1))
        .assign(cad_usd_lag=lambda df: df['cad_usd'].shift(periods=1))
        .reindex(columns=[
            'program_expenditure', 'debt_service', 'corporate_income_tax',
            'personal_income_tax', 'other_revenue', 'natural_resource_revenue',
            'deficit', 'heritage_dummy', 'ur_lag', 'er_lag', 'cad_usd_lag'
        ])
    )
    return df

mdfl = model_df_levels(df)
mdfl_err = model_df_levels(error_df)

Sumary statistics for key variables, 1970-71, 2016-17 in levels

Prior to any modeling, let’s compare the summary statistics for the data sets I’ve created against those in the paper:

number = "{:0<4,.1f}"
percent = '{:.1%}'
count = "{:0.0f}"


def tbl1_level(model_df: pd.DataFrame):
    """Produce summary statistics of the input data in levels.

    Parameters
    ----------
    model_df: pd.DataFrame
        Input data set

    Returns
    -------
    pd.io.formats.style.Styler:
        Nicely formatted summary statistics
    """
    df = (
        model_df
        .loc['1970':'2016']
        .copy()
        .drop(columns=['heritage_dummy'])
        .reindex(columns=[
            'natural_resource_revenue', 'corporate_income_tax', 'personal_income_tax',
            'other_revenue', 'debt_service', 'program_expenditure', 'deficit', 'ur_lag',
            'er_lag', 'cad_usd_lag'
        ])
        .describe()
        .T
        .style.format({
            'count': count,
            'mean': number,
            'std': number,
            'min': number,
            '25%': number,
            '50%': number,
            '75%': number,
            'max': number
        })
    )
    return df

Here’s Table 1 from the paper:

Image(filename="img/ferede_tbl_1.png")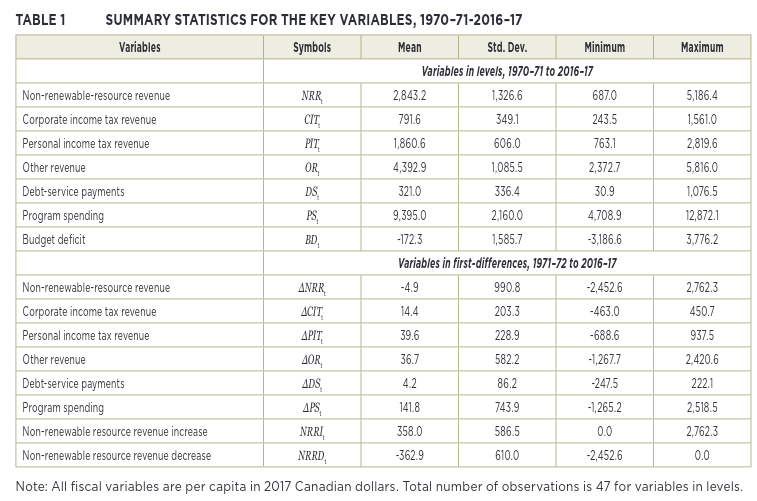

Here’s my summary of the top half

tbl1_level(mdfl)

	count	mean	std	min	25%	50%	75%	max
natural_resource_revenue	47	2,737.2	1,358.9	-125.3	1,726.4	2,371.7	3,941.6	5,181.6
corporate_income_tax	47	792.1	349.6	245.8	544.6	723.6	1,010.9	1,560.6
personal_income_tax	47	1,862.1	607.8	767.1	1,403.8	1,889.6	2,359.8	2,830.0
other_revenue	47	4,394.6	1,084.9	2,352.8	3,632.2	4,699.2	5,209.2	5,818.2
debt_service	47	322.8	334.9	31.4	82.7	158.5	486.9	1,075.6
program_expenditure	47	9,399.1	2,161.2	4,745.8	7,623.0	10,060.9	11,142.6	12,869.2
deficit	47	-64.0	1,618.0	-3,184.0	-1,320.5	-140.6	1,092.3	3,775.8
ur_lag	47	6.10	2.20	3.40	4.50	5.40	7.50	11.4
er_lag	47	63.7	9.90	38.5	65.1	67.3	69.0	71.8
cad_usd_lag	45	1.20	0.20	1.00	1.10	1.20	1.40	1.60

And the same summary on the data with the introduced error

tbl1_level(mdfl_err)

	count	mean	std	min	25%	50%	75%	max
natural_resource_revenue	47	2,843.8	1,325.6	691.9	1,760.7	2,532.1	3,972.6	5,181.6
corporate_income_tax	47	792.1	349.6	245.8	544.6	723.6	1,010.9	1,560.6
personal_income_tax	47	1,862.1	607.8	767.1	1,403.8	1,889.6	2,359.8	2,830.0
other_revenue	47	4,394.6	1,084.9	2,352.8	3,632.2	4,699.2	5,209.2	5,818.2
debt_service	47	322.8	334.9	31.4	82.7	158.5	486.9	1,075.6
program_expenditure	47	9,399.1	2,161.2	4,745.8	7,623.0	10,060.9	11,142.6	12,869.2
deficit	47	-170.7	1,587.7	-3,184.0	-1,425.7	-202.8	945.9	3,775.8
ur_lag	47	6.10	2.20	3.40	4.50	5.40	7.50	11.4
er_lag	47	63.7	9.90	38.5	65.1	67.3	69.0	71.8
cad_usd_lag	45	1.20	0.20	1.00	1.10	1.20	1.40	1.60

All the figures that I can validate against (exogenous variables aren’t reported in the paper) are reasonably close. The one noted difference is the previously described outlier in natural resource revenue which leads to my minimum for that variable being significantly lower than in the paper. That large one goes away again if I introduce the same data error described above. My guess for the remaining small discrepancies are differences in calculating population or CPI.

Sumary statistics for key variables, 1970-71, 2016-17, first difference

Reproduce the bottom half of table 1 from the paper

def model_df_first_diff(mdfl: pd.DataFrame) -> pd.DataFrame:
    """Produce the first difference of the level model df.

    Parameters
    ----------
    mdfl: pd.DataFrame
        The model dataframe in levels

    Returns
    -------
    pd.DataFrame
        The first differenced model dataframe
    """
    df = (
        mdfl
        .diff()
        .loc['1970':'2016']
        .copy()
        .assign(heritage_dummy=mdfl['heritage_dummy']) # don't want to lag diff this
        .assign(constant=1)
        .assign(zero=0)
        .assign(nrrd=lambda df: df[['natural_resource_revenue', 'zero']].min(axis='columns'))
        .assign(nrri=lambda df: df[['natural_resource_revenue', 'zero']].max(axis='columns'))
        .reindex(columns=[
            'natural_resource_revenue', 'nrri', 'nrrd', 'corporate_income_tax', 'personal_income_tax',
            'other_revenue', 'debt_service', 'program_expenditure', 'deficit', 'ur_lag',
            'er_lag', 'cad_usd_lag', 'heritage_dummy', 'constant'
        ])
    )
    return df

def tbl1_diff(model_df: pd.DataFrame) -> pd.io.formats.style.Styler:
    """Produce summary statistics of the first differenced data set.

    Parameters
    ----------
    model_df: pd.DataFrame
        Input data set

    Returns
    -------
    pd.io.formats.style.Styler:
        Nicely styled summary statistics
    """

    df = (
        model_df_first_diff(model_df)
        .drop(columns=['heritage_dummy', 'constant'])
        .describe()
        .T
        .style.format({
            'count': count,
            'mean': number,
            'std': number,
            'min': number,
            '25%': number,
            '50%': number,
            '75%': number,
            'max': number
        })
    )
    return df

Here’s Table 1 from the paper again:

Image(filename="img/ferede_tbl_1.png")

Here’s mine:

tbl1_diff(mdfl)

	count	mean	std	min	25%	50%	75%	max
natural_resource_revenue	47	-8.3	1,365.3	-4,543.2	-551.3	64.2	463.5	4,638.7
nrri	47	437.8	852.9	0.00	0.00	64.2	463.5	4,638.7
nrrd	47	-446.1	858.9	-4,543.2	-551.3	0.00	0.00	0.00
corporate_income_tax	47	13.3	201.2	-463.0	-108.5	25.9	137.8	447.1
personal_income_tax	47	42.7	227.2	-690.7	-28.7	40.0	154.2	936.9
other_revenue	47	41.8	577.2	-1,268.7	-288.9	-28.0	162.8	2,417.6
debt_service	47	4.50	86.2	-247.5	-21.6	2.00	36.0	222.3
program_expenditure	47	147.4	734.5	-1,263.2	-245.9	202.7	552.7	2,477.9
deficit	47	62.3	1,578.2	-4,722.8	-806.6	-39.0	836.0	4,431.3
ur_lag	47	0.10	1.10	-1.8	-0.7	-0.1	0.30	3.90
er_lag	47	0.60	3.30	-3.2	-0.2	0.40	0.90	21.4
cad_usd_lag	44	0.00	0.10	-0.2	-0.0	0.00	0.10	0.20

And with the data error:

tbl1_diff(mdfl_err)

	count	mean	std	min	25%	50%	75%	max
natural_resource_revenue	47	-8.3	977.5	-2,451.6	-471.1	64.2	458.3	2,757.8
nrri	47	349.1	579.4	0.00	0.00	64.2	458.3	2,757.8
nrrd	47	-357.4	604.0	-2,451.6	-471.1	0.00	0.00	0.00
corporate_income_tax	47	13.3	201.2	-463.0	-108.5	25.9	137.8	447.1
personal_income_tax	47	42.7	227.2	-690.7	-28.7	40.0	154.2	936.9
other_revenue	47	41.8	577.2	-1,268.7	-288.9	-28.0	162.8	2,417.6
debt_service	47	4.50	86.2	-247.5	-21.6	2.00	36.0	222.3
program_expenditure	47	147.4	734.5	-1,263.2	-245.9	202.7	552.7	2,477.9
deficit	47	62.3	1,260.2	-2,615.7	-758.1	-39.0	747.4	3,117.0
ur_lag	47	0.10	1.10	-1.8	-0.7	-0.1	0.30	3.90
er_lag	47	0.60	3.30	-3.2	-0.2	0.40	0.90	21.4
cad_usd_lag	44	0.00	0.10	-0.2	-0.0	0.00	0.10	0.20

As with everything so far, the data overall matches, and Natural Resource Revenue matches a lot better if I neglect to net out the heritage fund in 1976.

Unit-Root Tests

Table A1 in the paper shows the results of unit root tests for both the level and first differenced variables in the model. This section will reproduce those tables

def stationarity_tests(df: pd.DataFrame, first_diff: bool = False) -> pd.DataFrame:
    """Compute stationarity test statistics.

    Parameters
    ----------
    df: pd.DataFrame
        The model input data
    first_diff: bool, default False
        Perform tests on first differenced version of the data
    """
    if first_diff:
        df = (
            model_df_first_diff(df)
            .drop(columns=["heritage_dummy", "constant"])
        )
    else:
        df = (
            df
            .loc['1970':'2016']
            .copy()
            .drop(columns=['heritage_dummy'])
            .reindex(
                columns=[
                    'natural_resource_revenue',
                    'corporate_income_tax',
                    'personal_income_tax',
                    'other_revenue',
                    'debt_service',
                    'program_expenditure',
                    'deficit',
                    'ur_lag',
                    'er_lag',
                    'cad_usd_lag',
                ]
            )
        )
    tests_dict = {'ADF': ADF, 'Phillips-Perron': PhillipsPerron, 'DF-GLS': DFGLS}
    cols = df.columns
    tests_df = pd.DataFrame()
    for test_label, test in tests_dict.items():
        for col in cols:
            if test_label != 'Phillips-Perron':
                col_test = test(df[col].dropna(), method='BIC')
            else:
                col_test = test(df[col].dropna())
            test_val = col_test.stat
            test_p = col_test.pvalue
            test_summary = f'val: {test_val:0.3f}, p: {test_p:.1%}'
            tests_df.loc[col, test_label] = test_summary
    return tests_df

Here’s the table from the paper:

Image(filename="img/ferede_tbl_a1.png")

Here is mine with my data set

stationarity_tests(mdfl, first_diff=False)

	ADF	Phillips-Perron	DF-GLS
natural_resource_revenue	val: -3.927, p: 0.2%	val: -4.056, p: 0.1%	val: -3.125, p: 0.2%
corporate_income_tax	val: -2.340, p: 15.9%	val: -2.285, p: 17.7%	val: -1.676, p: 9.2%
personal_income_tax	val: -1.650, p: 45.7%	val: -1.440, p: 56.3%	val: -0.688, p: 43.2%
other_revenue	val: -2.196, p: 20.8%	val: -2.057, p: 26.2%	val: -1.585, p: 11.0%
debt_service	val: -1.548, p: 51.0%	val: -1.697, p: 43.3%	val: -1.377, p: 16.2%
program_expenditure	val: -2.966, p: 3.8%	val: -2.137, p: 23.0%	val: -0.682, p: 43.4%
deficit	val: -3.510, p: 0.8%	val: -3.924, p: 0.2%	val: -3.537, p: 0.0%
ur_lag	val: -2.709, p: 7.3%	val: -2.071, p: 25.6%	val: -2.319, p: 2.1%
er_lag	val: -10.652, p: 0.0%	val: -2.931, p: 4.2%	val: -0.763, p: 39.7%
cad_usd_lag	val: -2.454, p: 12.7%	val: -1.796, p: 38.2%	val: -1.870, p: 6.1%

stationarity_tests(mdfl, first_diff=True)

	ADF	Phillips-Perron	DF-GLS
natural_resource_revenue	val: -7.403, p: 0.0%	val: -10.300, p: 0.0%	val: -7.430, p: 0.0%
nrri	val: -6.885, p: 0.0%	val: -6.896, p: 0.0%	val: -6.533, p: 0.0%
nrrd	val: -7.835, p: 0.0%	val: -9.218, p: 0.0%	val: -7.634, p: 0.0%
corporate_income_tax	val: -7.228, p: 0.0%	val: -8.484, p: 0.0%	val: -7.103, p: 0.0%
personal_income_tax	val: -5.560, p: 0.0%	val: -8.831, p: 0.0%	val: -6.703, p: 0.0%
other_revenue	val: -7.914, p: 0.0%	val: -8.169, p: 0.0%	val: -7.717, p: 0.0%
debt_service	val: -3.918, p: 0.2%	val: -4.252, p: 0.1%	val: -3.931, p: 0.0%
program_expenditure	val: -2.545, p: 10.5%	val: -6.105, p: 0.0%	val: -2.461, p: 1.4%
deficit	val: -2.485, p: 11.9%	val: -10.105, p: 0.0%	val: -2.509, p: 1.2%
ur_lag	val: -4.924, p: 0.0%	val: -4.056, p: 0.1%	val: -4.901, p: 0.0%
er_lag	val: -2.697, p: 7.5%	val: -6.507, p: 0.0%	val: -2.742, p: 0.6%
cad_usd_lag	val: -3.318, p: 1.4%	val: -3.042, p: 3.1%	val: -3.384, p: 0.1%

And with the error data set:

stationarity_tests(mdfl_err, first_diff=False)

	ADF	Phillips-Perron	DF-GLS
natural_resource_revenue	val: -2.652, p: 8.3%	val: -2.875, p: 4.8%	val: -2.113, p: 3.5%
corporate_income_tax	val: -2.340, p: 15.9%	val: -2.285, p: 17.7%	val: -1.676, p: 9.2%
personal_income_tax	val: -1.650, p: 45.7%	val: -1.440, p: 56.3%	val: -0.688, p: 43.2%
other_revenue	val: -2.196, p: 20.8%	val: -2.057, p: 26.2%	val: -1.585, p: 11.0%
debt_service	val: -1.548, p: 51.0%	val: -1.697, p: 43.3%	val: -1.377, p: 16.2%
program_expenditure	val: -2.966, p: 3.8%	val: -2.137, p: 23.0%	val: -0.682, p: 43.4%
deficit	val: -2.566, p: 10.0%	val: -2.763, p: 6.4%	val: -2.606, p: 0.9%
ur_lag	val: -2.709, p: 7.3%	val: -2.071, p: 25.6%	val: -2.319, p: 2.1%
er_lag	val: -10.652, p: 0.0%	val: -2.931, p: 4.2%	val: -0.763, p: 39.7%
cad_usd_lag	val: -2.454, p: 12.7%	val: -1.796, p: 38.2%	val: -1.870, p: 6.1%

stationarity_tests(mdfl_err, first_diff=True)

	ADF	Phillips-Perron	DF-GLS
natural_resource_revenue	val: -5.913, p: 0.0%	val: -7.791, p: 0.0%	val: -5.925, p: 0.0%
nrri	val: -6.119, p: 0.0%	val: -6.149, p: 0.0%	val: -5.731, p: 0.0%
nrrd	val: -7.846, p: 0.0%	val: -8.008, p: 0.0%	val: -7.640, p: 0.0%
corporate_income_tax	val: -7.228, p: 0.0%	val: -8.484, p: 0.0%	val: -7.103, p: 0.0%
personal_income_tax	val: -5.560, p: 0.0%	val: -8.831, p: 0.0%	val: -6.703, p: 0.0%
other_revenue	val: -7.914, p: 0.0%	val: -8.169, p: 0.0%	val: -7.717, p: 0.0%
debt_service	val: -3.918, p: 0.2%	val: -4.252, p: 0.1%	val: -3.931, p: 0.0%
program_expenditure	val: -2.545, p: 10.5%	val: -6.105, p: 0.0%	val: -2.461, p: 1.4%
deficit	val: -6.642, p: 0.0%	val: -8.574, p: 0.0%	val: -6.609, p: 0.0%
ur_lag	val: -4.924, p: 0.0%	val: -4.056, p: 0.1%	val: -4.901, p: 0.0%
er_lag	val: -2.697, p: 7.5%	val: -6.507, p: 0.0%	val: -2.742, p: 0.6%
cad_usd_lag	val: -3.318, p: 1.4%	val: -3.042, p: 3.1%	val: -3.384, p: 0.1%

Documentation on the test tools I used can be found here

There are some interesting differences. Most notable is that on the levels of the deficit series I reject the null hypothesis of a unit root using all three tests at a significance level < 1%. The paper specifically notes that if the deficit is stationary in levels then a Vector Error Correction model can be applied. As the original author’s fails to reject the null he implements a Vector AutoRegression model on the first differenced data. In levels the only other series that I find to be stationary is natural resource revenue. ADF on program expenditure would also reject the null at 5% significance, but would fail to reject it using the other two tests.

Looking at the first differenced series, since that’s what the paper ultimately ends up using, I also reject the null hypothesis of a unit root for all variables using all tests at a 1% significant except program expenditure and deficit using Augmented Dickey Fuller. Those last two tests differ from what’s reported in the paper.

The paper notes that it uses the Schwarz Information Criterion (SIC) for determining optimal lags in the DF-GLS test. It doesn’t specify what it’s using in the other two tests. For ADF and DF-GLS I used the Schwarz/Bayesian IC (BIC), which is just another name for SIC. Phillips-Perron only uses 1 lag and then Newey-West for a long run variance estimator. I also ran these tests using Akaike IC (AIC) for optimal lags for ADF and DF-GLS, with similar results.

Again we can see that using the results with the data error more closely matches the table in the paper, specifically around resource revenue and deficits.

The Model

The conclusions from the paper are based on fitting a VAR to the first differenced data set we’ve been analyzing above. Let’s do that now and compare the results to the paper.

def fit_var(mdfl: pd.DataFrame) -> statsmodels.tsa.vector_ar.var_model.VARResults:
    """Fit a VAR to the model data.

    Parameters
    ----------
    mdfl: pd.DataFrame
        Input model data

    Returns
    -------
    statsmodels.tsa.vector_ar.var_model.VarResults
        The fitted model
    """
    vec_df = (
        model_df_first_diff(mdfl)
        .drop(columns='natural_resource_revenue')
        .dropna()
    )
    endog_df = vec_df[[
        'nrri', 'nrrd', 'program_expenditure', 'debt_service', 'corporate_income_tax',
         'personal_income_tax', 'other_revenue'
    ]]
    exog_df = vec_df[['ur_lag', 'er_lag', 'cad_usd_lag', 'heritage_dummy']]
    model = VAR(endog=endog_df, exog=exog_df, freq='AS')
    # Fit the model with 2 lags
    results = model.fit(2)
    return results

def highlight_significance(val):
    """Colour code statistical significance.

    Takes a scalar and returns a string with
    the css property `'color: <color>'` where
    color is maroon for 1% significance, 
    red for 5% significance,
    orange for 10%, and black otherwise

    Parameters
    ----------
    val: float
        The p value of a test

    Returns
    -------
    str:
        A formatted colour coded p value
    """

    if val <= 0.01:
        color = 'maroon'
    elif val <= 0.05:
        color = 'red'
    elif val <= 0.1:
        color = 'orange'
    else:
        color = 'black'
    return f'color: {color}'

results = fit_var(mdfl)
results_err = fit_var(mdfl_err)
summary = results.summary()

# Set up the rows and columns of my parameters to match the paper
reindex_cols = ["program_expenditure", "debt_service", "corporate_income_tax", "personal_income_tax", "other_revenue", "nrri", "nrrd"]
index_order = ["nrri", "nrrd", "program_expenditure", "debt_service", "corporate_income_tax", "personal_income_tax", "other_revenue"]
reindex_rows = list(chain.from_iterable((f"L1.{row}", f"L2.{row}") for row in index_order))

Here’s the table from the paper:

Image(filename="img/ferede_tbl_a2.png")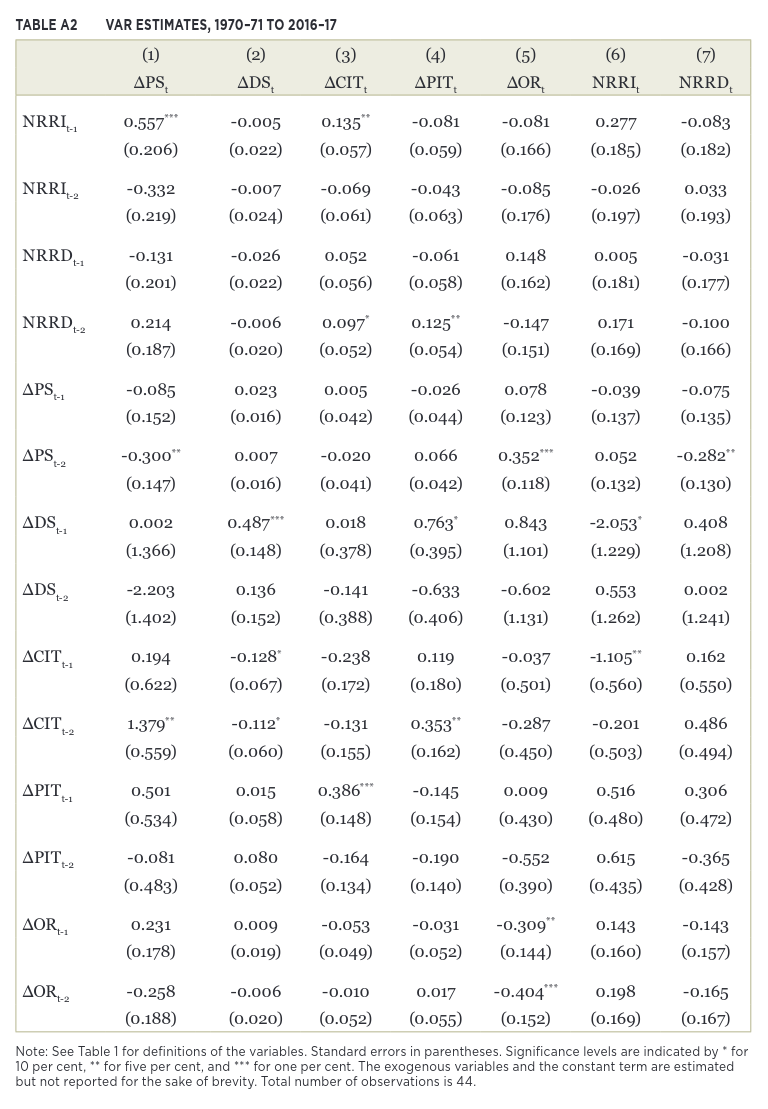

results.params.reindex(index=reindex_rows, columns=reindex_cols)

	program_expenditure	debt_service	corporate_income_tax	personal_income_tax	other_revenue	nrri	nrrd
L1.nrri	0.307014	-0.028267	0.081846	-0.052581	-0.197417	0.157775	0.002814
L2.nrri	0.328607	0.006210	-0.044256	-0.031283	-0.073461	0.059988	-0.052033
L1.nrrd	0.131802	-0.034380	0.026578	-0.144894	0.193682	-0.067386	-0.333322
L2.nrrd	0.353466	-0.020362	0.089569	-0.037287	-0.147460	0.110970	-0.055394
L1.program_expenditure	-0.089949	0.024739	-0.000802	-0.053868	0.070080	-0.065026	-0.105625
L2.program_expenditure	-0.262484	0.009716	-0.031223	0.042743	0.410439	0.025392	-0.456895
L1.debt_service	0.794685	0.401266	-0.108643	0.336733	0.400447	-2.370450	-0.278888
L2.debt_service	-2.693856	0.228409	-0.088742	-0.179124	-0.041884	0.290135	-0.215989
L1.corporate_income_tax	-0.972853	-0.092308	-0.210123	0.169059	-0.071714	-0.914462	0.730905
L2.corporate_income_tax	0.088413	-0.199031	-0.206852	0.245321	-0.509617	-0.683630	-0.578293
L1.personal_income_tax	0.959002	-0.041882	0.292569	-0.378646	-0.250158	0.347750	0.862515
L2.personal_income_tax	0.814557	0.084507	-0.112748	-0.099020	-0.528812	0.385575	-0.226230
L1.other_revenue	0.347131	-0.015834	-0.042866	-0.022883	-0.296401	0.224576	-0.102018
L2.other_revenue	-0.140592	-0.010601	-0.009822	-0.010749	-0.339955	0.385613	0.043835

results.pvalues.reindex(index=reindex_rows, columns=reindex_cols).style.applymap(highlight_significance).format("{:.2%}")

	program_expenditure	debt_service	corporate_income_tax	personal_income_tax	other_revenue	nrri	nrrd
L1.nrri	17.85%	28.23%	19.05%	46.54%	31.40%	35.35%	99.27%
L2.nrri	3.41%	72.82%	29.76%	52.28%	58.14%	60.37%	80.42%
L1.nrrd	54.73%	17.31%	65.78%	3.61%	30.34%	67.97%	26.07%
L2.nrrd	8.86%	39.46%	11.53%	56.93%	40.83%	47.32%	84.37%
L1.program_expenditure	63.72%	26.03%	98.78%	37.09%	66.89%	64.73%	68.24%
L2.program_expenditure	16.67%	65.69%	54.83%	47.56%	1.18%	85.75%	7.53%
L1.debt_service	62.80%	3.37%	80.89%	51.54%	77.63%	5.24%	90.00%
L2.debt_service	9.99%	22.60%	84.32%	72.89%	97.63%	81.21%	92.24%
L1.corporate_income_tax	17.66%	26.58%	28.68%	45.69%	90.77%	8.83%	45.31%
L2.corporate_income_tax	90.24%	1.66%	29.52%	28.12%	41.09%	20.34%	55.35%
L1.personal_income_tax	11.91%	55.47%	8.27%	5.12%	63.61%	44.83%	30.03%
L2.personal_income_tax	12.28%	16.47%	43.56%	55.23%	24.36%	32.70%	75.15%
L1.other_revenue	11.25%	52.98%	47.45%	74.03%	11.48%	16.83%	73.04%
L2.other_revenue	54.20%	68.98%	87.64%	88.26%	8.61%	2.48%	88.83%

results_err.params.reindex(index=reindex_rows, columns=reindex_cols)

	program_expenditure	debt_service	corporate_income_tax	personal_income_tax	other_revenue	nrri	nrrd
L1.nrri	0.531582	-0.024542	0.107731	-0.123072	-0.150617	0.208281	-0.080868
L2.nrri	-0.184916	-0.003392	-0.079855	-0.031832	-0.134564	0.023580	0.076075
L1.nrrd	-0.164689	-0.033454	0.002593	-0.085661	0.110608	-0.058941	-0.105753
L2.nrrd	0.179398	-0.020179	0.072508	0.027891	-0.178763	0.081864	-0.032297
L1.program_expenditure	-0.148569	0.024375	0.010583	-0.035676	0.095480	-0.051153	-0.027252
L2.program_expenditure	-0.274168	0.012469	-0.028204	0.060072	0.419366	0.043190	-0.266589
L1.debt_service	-0.138827	0.391381	-0.192682	0.456206	0.250624	-2.379002	0.182134
L2.debt_service	-1.839879	0.244616	0.030729	-0.321701	0.208719	0.387627	0.026273
L1.corporate_income_tax	-0.591167	-0.087419	-0.166213	0.193455	-0.009423	-1.069105	0.084121
L2.corporate_income_tax	0.986182	-0.171169	-0.180347	0.219469	-0.439124	-0.441616	0.337464
L1.personal_income_tax	0.446547	-0.050872	0.281996	-0.364826	-0.291701	0.365623	0.499642
L2.personal_income_tax	0.537147	0.068406	-0.161794	-0.159843	-0.598672	0.542697	-0.054906
L1.other_revenue	0.319686	-0.014068	-0.036482	-0.021636	-0.280981	0.235076	-0.052564
L2.other_revenue	-0.328932	-0.009975	-0.017606	0.013375	-0.362590	0.255418	-0.122366

results_err.pvalues.reindex(index=reindex_rows, columns=reindex_cols).style.applymap(highlight_significance).format("{:.2%}")

	program_expenditure	debt_service	corporate_income_tax	personal_income_tax	other_revenue	nrri	nrrd
L1.nrri	6.09%	42.34%	12.95%	12.90%	50.73%	26.95%	75.32%
L2.nrri	53.56%	91.63%	28.56%	70.91%	57.36%	90.54%	77.87%
L1.nrrd	54.19%	25.17%	96.94%	26.71%	60.91%	74.28%	66.59%
L2.nrrd	49.68%	47.94%	27.30%	71.17%	39.79%	64.10%	89.27%
L1.program_expenditure	47.97%	28.33%	84.07%	55.26%	57.06%	71.44%	88.63%
L2.program_expenditure	18.15%	57.39%	58.33%	30.58%	1.07%	75.16%	15.20%
L1.debt_service	93.96%	4.82%	67.48%	38.39%	86.44%	5.10%	91.27%
L2.debt_service	31.50%	21.64%	94.66%	53.88%	88.68%	75.02%	98.74%
L1.corporate_income_tax	47.78%	33.14%	42.56%	41.64%	98.87%	5.35%	91.13%
L2.corporate_income_tax	17.90%	3.09%	32.66%	29.54%	45.50%	36.55%	61.21%
L1.personal_income_tax	51.65%	49.41%	10.20%	6.37%	59.67%	42.44%	42.34%
L2.personal_income_tax	39.82%	31.95%	30.98%	37.91%	23.97%	19.93%	92.41%
L1.other_revenue	16.84%	57.49%	53.04%	74.43%	13.07%	12.78%	80.28%
L2.other_revenue	18.72%	71.13%	77.81%	85.12%	6.95%	12.35%	58.85%

Once again, my results with the data error included are much closer to the original paper results. Note that without the data error, program spending is shown to rise in response to an increase or decrease in natural resource revenue, but only on the second lag (at least at a statistically significant level. That’s completely contrary to the main thesis of the paper. Now, given that I’ve shown with the corrected data set that budget deficits are stationary in levels, maybe a more appropriate form of analysis would have been to use a VECM as the paper states it would have been, but from this I can say that the data error has led to a significant change in the outcome of the analysis.

Impulse Response Functions

The actual results of the paper involve taking the estimated impulse response functions derived from the VAR model and examining their implications. Given the results above I’m not sure there’s a lot of value in reproducing all of the other results of this model, but I do want to at least reproduce the IRFs.

def irf_tbl(result: statsmodels.tsa.vector_ar.var_model.VARResults, impulse: str) -> pd.DataFrame:
    """Show the IRF as in table 3 of the paper.

    Parameters
    ----------
    result: statsmodels.tsa.vector_ar.var_model.VARResults
        The fitted VAR

    impulse: str
        The impulse function, either an increase or decrease in natural resource revenue

    Returns
    -------
    pd.DataFrame
        A summary table
    """
    irf = result.irf()
    irf_stderr = irf.stderr()
    irfs = irf.irfs
    params = list(results.params.columns)

    def _impulse_response(impulse: str, response: str) -> pd.DataFrame:
        """Get a specific IRF out of the big array.

        Parameters
        ----------
        impulse: str
            The impulse function
        response: str
            The response function

        Returns
        -------
        pd.DataFrame
            The 3 period IRF
        """
        imp_ind = params.index(impulse)
        res_ind = params.index(response)
        ir = irfs[:, res_ind, imp_ind]
        se = irf_stderr[:, res_ind, imp_ind]
        imp_name = response + '_impulse'
        se_name = response + '_se'
        df = pd.DataFrame({imp_name: ir, se_name: se})
        return df.loc[1:3].T

    responses = params[2:]
    return pd.concat([_impulse_response(impulse, response) for response in responses])

Table 3

IMPACTS ON ALBERTA’S BUDGET OF A ONE-DOLLAR INNOVATION IN NON-RENEWABLE-RESOURCE REVENUE (ASYMMETRIC CASE), 1970/71–2016/17

Image(filename="img/ferede_tbl_3.png")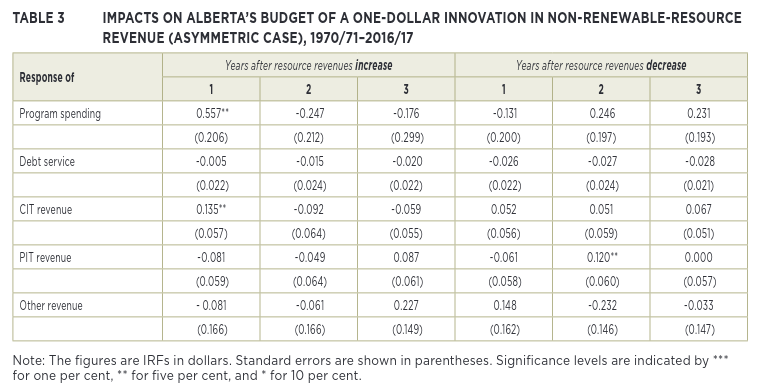

irf_tbl(results, "nrrd")

	1	2	3
program_expenditure_impulse	0.131802	0.152091	-0.263057
program_expenditure_se	0.219009	0.213435	0.189561
debt_service_impulse	-0.034380	-0.016984	-0.025572
debt_service_se	0.025235	0.026153	0.023777
corporate_income_tax_impulse	0.026578	0.022545	0.014045
corporate_income_tax_se	0.060010	0.062050	0.049948
personal_income_tax_impulse	-0.144894	0.050801	0.023045
personal_income_tax_se	0.069135	0.090279	0.082072
other_revenue_impulse	0.193682	-0.226313	0.116648
other_revenue_se	0.188179	0.190130	0.169276

irf_tbl(results, "nrri")

	1	2	3
program_expenditure_impulse	0.307014	0.128759	0.032942
program_expenditure_se	0.228184	0.200129	0.172849
debt_service_impulse	-0.028267	-0.004321	-0.011658
debt_service_se	0.026292	0.026157	0.025746
corporate_income_tax_impulse	0.081846	-0.052562	-0.019982
corporate_income_tax_se	0.062524	0.057369	0.041195
personal_income_tax_impulse	-0.052581	-0.027779	0.040890
personal_income_tax_se	0.072031	0.085436	0.068562
other_revenue_impulse	-0.197417	-0.028068	0.187637
other_revenue_se	0.196063	0.172347	0.147472

irf_tbl(results_err, "nrrd")

	1	2	3
program_expenditure_impulse	-0.164689	0.190170	0.024520
program_expenditure_se	0.270039	0.264733	0.231589
debt_service_impulse	-0.033454	-0.029727	-0.027865
debt_service_se	0.029185	0.033489	0.028892
corporate_income_tax_impulse	0.002593	0.041965	0.055297
corporate_income_tax_se	0.067657	0.068952	0.054178
personal_income_tax_impulse	-0.085661	0.064177	-0.029006
personal_income_tax_se	0.077188	0.085444	0.072486
other_revenue_impulse	0.110608	-0.211807	-0.018863
other_revenue_se	0.216285	0.206303	0.197149

irf_tbl(results_err, "nrri")

	1	2	3
program_expenditure_impulse	0.531582	-0.303243	-0.034754
program_expenditure_se	0.283645	0.282106	0.247443
debt_service_impulse	-0.024542	-0.003484	-0.020839
debt_service_se	0.030655	0.033327	0.030126
corporate_income_tax_impulse	0.107731	-0.094389	-0.033291
corporate_income_tax_se	0.071066	0.074045	0.058701
personal_income_tax_impulse	-0.123072	-0.011699	0.079664
personal_income_tax_se	0.081077	0.093111	0.078465
other_revenue_impulse	-0.150617	-0.053069	0.289039
other_revenue_se	0.227183	0.225741	0.202924

Same patters as we’ve seen above, the results with the data error included are pretty close to what the paper reports.

Plot the IRFs

Ok, this is the last bit I want to reproduce, just because IRF charts look cool so it would be a shame to leave them out.

Image(filename="img/ferede_fig_3.png")

results.irf().plot(impulse='nrri', response='program_expenditure');

results.irf().plot(impulse='nrrd', response='program_expenditure');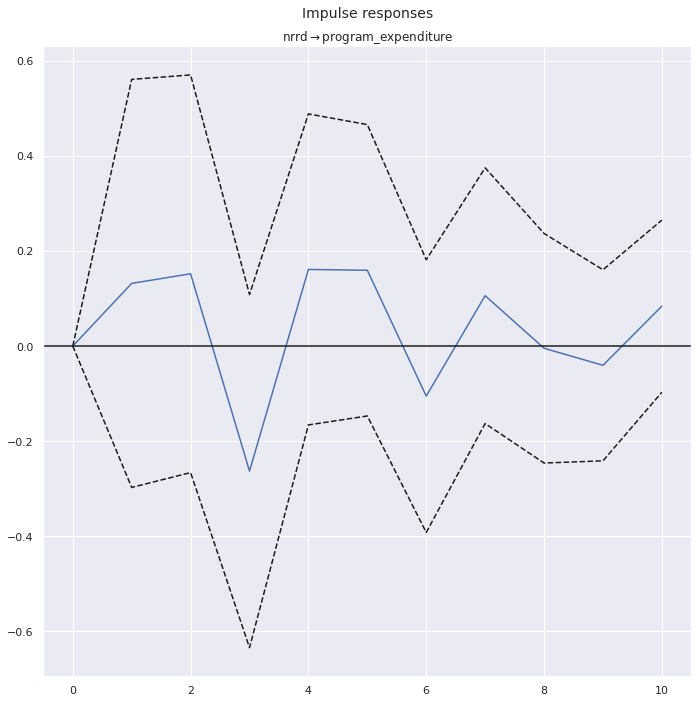

results_err.irf().plot(impulse='nrri', response='program_expenditure');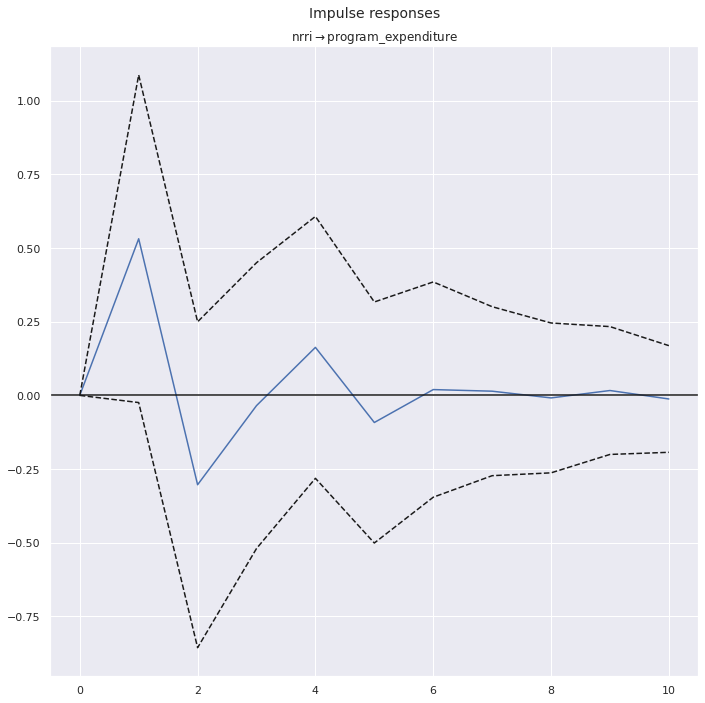

results_err.irf().plot(impulse='nrrd', response='program_expenditure');

These are harder to eyeball because I’m showing the individual responses and the paper is showing the cumulative ones. But again, if I think about what adding up the points in my charts would look like, they end up closer to the data set with the error.

Conclusion

The initial goal of this exercise was to practice my python and econometrics. I’ve certainly done that over the course of working on it, but as a bonus I’ve also demonstrated how sensitive results can be to even a single data point (at least when you have relatively few samples.

Appendix: Raw tables

For the purposes of validation, here are the full tables I used to produce both the summary statistics above, as well as all statistical models and tests below

mdfl

	program_expenditure	debt_service	corporate_income_tax	personal_income_tax	other_revenue	natural_resource_revenue	deficit	heritage_dummy	ur_lag	er_lag	cad_usd_lag
budget_dt
1964-01-01	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
1965-01-01	2327.844291	11.272854	174.729232	231.093501	1442.925275	1397.833860	-907.464724	0.0	2.500000	37.935748	NaN
1966-01-01	2891.984579	10.750872	145.136773	301.024417	1542.750138	1290.104645	-376.280521	0.0	2.500000	37.935748	NaN
1967-01-01	4436.875339	10.199713	203.994268	407.988537	2351.033944	1116.868620	367.189683	0.0	2.500000	37.935748	NaN
1968-01-01	4368.535726	19.160244	239.503055	469.425988	2639.323668	1360.377353	-320.934094	0.0	2.700000	38.322148	NaN
1969-01-01	4396.849967	17.909776	286.556413	599.977490	2444.684401	1141.748209	-58.206771	0.0	3.300000	39.041995	NaN
1970-01-01	4745.762712	38.135593	245.762712	771.186441	2737.288136	978.813559	50.847458	0.0	3.400000	39.833226	NaN
1971-01-01	4993.823780	67.916003	271.664014	767.051333	2848.477084	1090.651114	83.896240	0.0	5.200000	39.686520	NaN
1972-01-01	4988.477844	85.114978	362.663820	858.551083	2768.087112	1224.915554	-140.624746	0.0	5.700000	38.456938	1.009883
1973-01-01	5004.356719	81.151731	382.089398	977.202089	2387.213408	2160.664826	-821.661272	0.0	5.700000	39.470588	0.990792
1974-01-01	6124.378806	92.793618	829.155879	1038.689856	2352.767225	4549.880638	-2553.321174	0.0	5.300000	40.843443	1.000233
1975-01-01	7071.218716	84.149869	686.347373	925.648564	2721.722340	4417.868145	-1596.217836	0.0	3.500000	42.840909	0.978133
1976-01-01	6845.363213	59.113672	326.307469	1038.036080	2830.362613	-125.320985	2835.091707	1.0	4.200000	43.439912	1.017267
1977-01-01	7061.151803	46.247496	554.969954	1206.639219	2720.193639	4513.335196	-1887.738708	1.0	3.891667	64.800000	0.986075
1978-01-01	6825.084687	48.260049	545.709790	1225.062794	2643.165786	4701.642511	-2242.236144	1.0	4.475000	64.633333	1.063525
1979-01-01	9302.990086	32.774318	342.491620	1265.088664	2525.261181	5181.619632	21.303307	1.0	4.750000	65.341667	1.140767
1980-01-01	9937.742745	31.376340	620.395823	1337.773062	2676.972321	4797.727697	536.250183	1.0	3.966667	67.125000	1.171558
1981-01-01	10441.551444	109.885646	701.577586	1597.568239	5094.588359	4001.769572	-844.066666	1.0	3.866667	68.050000	1.169408
1982-01-01	12281.969722	57.716023	639.073783	1731.480694	4808.269418	2887.899921	2272.961929	1.0	3.883333	69.500000	1.198892
1983-01-01	11489.190564	168.596206	771.007210	1488.773513	4813.372379	4001.941517	582.692150	1.0	7.750000	66.275000	1.233858
1984-01-01	11320.287262	218.545766	793.666203	1396.584127	5529.782999	4306.693537	-487.893837	1.0	11.008333	63.816667	1.232583
1985-01-01	12869.198063	168.831114	723.561918	1410.945740	5622.447161	3939.701880	1341.372479	1.0	11.408333	63.933333	1.295150
1986-01-01	11863.166376	263.862833	351.817111	1570.739021	4940.542816	1488.115306	3775.814955	1.0	9.775000	65.491667	1.365900
1987-01-01	10791.884860	486.136253	505.683690	1900.350807	5480.081397	2231.807343	1160.097876	0.0	10.008333	65.350000	1.389767
1988-01-01	10774.989850	655.047057	572.857965	1675.835569	5818.165763	1713.642551	1649.535059	0.0	9.525000	65.450000	1.326175
1989-01-01	10745.455671	865.692419	543.484030	1968.964999	5716.675586	1739.148895	1642.874581	0.0	7.983333	66.925000	1.230942
1990-01-01	10614.752643	923.523101	578.462597	2014.173627	5689.536231	1936.372929	1319.730359	0.0	7.158333	67.516667	1.184108
1991-01-01	10060.915107	878.291420	488.608088	2043.330951	5298.490171	1351.526066	1757.251250	0.0	6.916667	67.500000	1.167017
1992-01-01	10490.255898	920.232018	413.099221	1811.929709	5614.128666	1415.691681	2155.638638	0.0	8.250000	66.591667	1.145975
1993-01-01	9567.673764	1046.414892	540.289188	1820.154561	5604.076850	1782.195133	867.372924	0.0	9.458333	65.383333	1.208808
1994-01-01	8304.447335	1075.635389	661.029079	1886.982358	5328.892392	2081.040289	-577.861395	0.0	9.583333	64.875000	1.290167
1995-01-01	7542.256294	1000.994980	792.231321	1889.578759	4888.995090	1657.024370	-684.578266	0.0	8.783333	65.725000	1.365892
1996-01-01	7286.510699	838.743299	807.190029	1976.382124	4455.321793	2314.288966	-1427.928914	0.0	7.841667	66.650000	1.372650
1997-01-01	7598.400009	729.331650	1020.071271	2138.894710	4551.426710	2084.277589	-1466.938621	0.0	6.883333	67.316667	1.363700
1998-01-01	7647.600932	735.120709	884.383797	2452.712386	4366.478407	1262.339259	-583.192208	0.0	5.875000	67.925000	1.384867
1999-01-01	8342.393922	487.608742	640.113987	2601.260027	4640.443868	2371.737084	-1423.552301	0.0	5.583333	68.566667	1.483633
2000-01-01	8710.352822	474.863472	980.253881	1910.598641	4348.877202	5129.494603	-3184.008033	0.0	5.666667	68.500000	1.485825
2001-01-01	9338.287124	360.113309	1037.070500	1946.193764	4320.894451	2897.190669	-502.948950	0.0	4.966667	68.675000	1.485517
2002-01-01	8826.496403	209.515399	888.679810	2127.725707	3820.134757	3138.329395	-938.857868	0.0	4.725000	68.975000	1.549017
2003-01-01	8889.845744	112.157737	701.917057	1909.164731	4925.835384	3176.836868	-1711.750559	0.0	5.341667	68.975000	1.570592
2004-01-01	9563.476337	121.092191	947.887219	1864.098004	5040.562703	3907.027522	-2075.006920	0.0	5.116667	69.741667	1.401167
2005-01-01	10252.960247	95.080363	1118.344428	1793.108293	5214.467798	4829.545684	-2607.425593	1.0	4.591667	70.125000	1.301575
2006-01-01	10491.526962	77.006633	1291.562414	2729.974686	5203.857546	3943.455955	-2600.317006	1.0	3.941667	69.850000	1.211483
2007-01-01	11093.119793	71.131049	1560.562037	2749.181812	4712.930591	3359.113940	-1217.537538	1.0	3.458333	70.791667	1.134375
2008-01-01	11481.223206	65.508008	1339.134853	2742.517945	3444.209491	3752.538047	268.330878	0.0	3.566667	71.383333	1.074183
2009-01-01	11192.177199	111.838586	1464.684956	2426.866512	5009.321141	2085.188848	317.954328	0.0	3.691667	71.800000	1.066767
2010-01-01	11408.370379	141.808459	1001.672465	2292.670240	4699.207866	2532.122236	1024.506031	0.0	6.575000	69.416667	1.141442
2011-01-01	11288.615235	144.188676	1062.777455	2474.323912	4526.773140	3362.283433	6.645971	0.0	6.516667	68.133333	1.030125
2012-01-01	11491.360391	143.201492	1330.207614	2690.901483	4642.860889	2175.711738	794.880159	0.0	5.433333	69.508333	0.989025
2013-01-01	11803.343431	158.459375	1473.940765	2829.977012	5288.245930	2572.413384	-202.774285	0.0	4.700000	69.958333	0.999408
2014-01-01	11006.721496	182.199224	1479.028999	2817.708454	4975.008515	2283.359468	-366.184716	0.0	4.658333	69.591667	1.029992
2015-01-01	10664.784806	176.142114	1040.727000	2817.529567	4492.864354	691.915996	1797.890004	0.0	4.775000	69.058333	1.104683
2016-01-01	11322.810385	230.029051	913.571647	2608.854241	4407.637789	750.684901	2872.090858	0.0	6.091667	68.408333	1.278808
2017-01-01	11433.853017	319.856119	813.921696	2543.505301	5094.564399	1175.559759	2126.157981	0.0	8.133333	66.250000	1.325583
2018-01-01	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	7.883333	66.316667	1.297858

model_df_first_diff(mdfl)

	natural_resource_revenue	nrri	nrrd	corporate_income_tax	personal_income_tax	other_revenue	debt_service	program_expenditure	deficit	ur_lag	er_lag	cad_usd_lag	heritage_dummy	constant
budget_dt
1970-01-01	-162.934650	0.000000	-162.934650	-40.793701	171.208950	292.603734	20.225817	348.912745	109.054229	0.100000	0.791232	NaN	0.0	1
1971-01-01	111.837554	111.837554	0.000000	25.901302	-4.135108	111.188949	29.780410	248.061068	33.048782	1.800000	-0.146706	NaN	0.0	1
1972-01-01	134.264440	134.264440	0.000000	90.999806	91.499750	-80.389972	17.198975	-5.345936	-224.520986	0.500000	-1.229583	NaN	0.0	1
1973-01-01	935.749273	935.749273	0.000000	19.425579	118.651006	-380.873704	-3.963247	15.878875	-681.036526	0.000000	1.013650	-0.019092	0.0	1
1974-01-01	2389.215812	2389.215812	0.000000	447.066481	61.487767	-34.446183	11.641888	1120.022088	-1731.659902	-0.400000	1.372855	0.009442	0.0	1
1975-01-01	-132.012493	0.000000	-132.012493	-142.808507	-113.041292	368.955115	-8.643749	946.839909	957.103338	-1.800000	1.997466	-0.022100	0.0	1
1976-01-01	-4543.189130	0.000000	-4543.189130	-360.039903	112.387516	108.640274	-25.036197	-225.855503	4431.309543	0.700000	0.599003	0.039133	1.0	1
1977-01-01	4638.656180	4638.656180	0.000000	228.662485	168.603139	-110.168974	-12.866176	215.788591	-4722.830415	-0.308333	21.360088	-0.031192	1.0	1
1978-01-01	188.307315	188.307315	0.000000	-9.260164	18.423575	-77.027853	2.012553	-236.067116	-354.497436	0.583333	-0.166667	0.077450	1.0	1
1979-01-01	479.977121	479.977121	0.000000	-203.218170	40.025870	-117.904605	-15.485732	2477.905398	2263.539451	0.275000	0.708333	0.077242	1.0	1
1980-01-01	-383.891935	0.000000	-383.891935	277.904203	72.684398	151.711140	-1.397977	634.752660	514.946876	-0.783333	1.783333	0.030792	1.0	1
1981-01-01	-795.958126	0.000000	-795.958126	81.181763	259.795177	2417.616038	78.509306	503.808699	-1380.316848	-0.100000	0.925000	-0.002150	1.0	1
1982-01-01	-1113.869651	0.000000	-1113.869651	-62.503803	133.912455	-286.318941	-52.169623	1840.418278	3117.028595	0.016667	1.450000	0.029483	1.0	1
1983-01-01	1114.041596	1114.041596	0.000000	131.933427	-242.707181	5.102961	110.880183	-792.779158	-1690.269779	3.866667	-3.225000	0.034967	1.0	1
1984-01-01	304.752020	304.752020	0.000000	22.658992	-92.189386	716.410620	49.949560	-168.903301	-1070.585987	3.258333	-2.458333	-0.001275	1.0	1
1985-01-01	-366.991657	0.000000	-366.991657	-70.104285	14.361613	92.664162	-49.714652	1548.910801	1829.266316	0.400000	0.116667	0.062567	1.0	1
1986-01-01	-2451.586574	0.000000	-2451.586574	-371.744807	159.793281	-681.904345	95.031719	-1006.031688	2434.442476	-1.633333	1.558333	0.070750	1.0	1
1987-01-01	743.692037	743.692037	0.000000	153.866579	329.611786	539.538581	222.273420	-1071.281516	-2615.717079	0.233333	-0.141667	0.023867	0.0	1
1988-01-01	-518.164793	0.000000	-518.164793	67.174276	-224.515238	338.084366	168.910804	-16.895010	489.437183	-0.483333	0.100000	-0.063592	0.0	1
1989-01-01	25.506344	25.506344	0.000000	-29.373936	293.129430	-101.490177	210.645362	-29.534180	-6.660479	-1.541667	1.475000	-0.095233	0.0	1
1990-01-01	197.224034	197.224034	0.000000	34.978568	45.208628	-27.139354	57.830682	-130.703028	-323.144222	-0.825000	0.591667	-0.046833	0.0	1
1991-01-01	-584.846863	0.000000	-584.846863	-89.854509	29.157325	-391.046061	-45.231681	-553.837536	437.520891	-0.241667	-0.016667	-0.017092	0.0	1
1992-01-01	64.165615	64.165615	0.000000	-75.508867	-231.401242	315.638496	41.940598	429.340791	398.387388	1.333333	-0.908333	-0.021042	0.0	1
1993-01-01	366.503452	366.503452	0.000000	127.189967	8.224851	-10.051816	126.182874	-922.582134	-1288.265714	1.208333	-1.208333	0.062833	0.0	1
1994-01-01	298.845156	298.845156	0.000000	120.739891	66.827798	-275.184458	29.220498	-1263.226429	-1445.234319	0.125000	-0.508333	0.081358	0.0	1
1995-01-01	-424.015919	0.000000	-424.015919	131.202242	2.596401	-439.897302	-74.640409	-762.191041	-106.716872	-0.800000	0.850000	0.075725	0.0	1
1996-01-01	657.264596	657.264596	0.000000	14.958707	86.803365	-433.673297	-162.251681	-255.745595	-743.350647	-0.941667	0.925000	0.006758	0.0	1
1997-01-01	-230.011377	0.000000	-230.011377	212.881242	162.512585	96.104917	-109.411649	311.889310	-39.009707	-0.958333	0.666667	-0.008950	0.0	1
1998-01-01	-821.938330	0.000000	-821.938330	-135.687474	313.817676	-184.948302	5.789059	49.200923	883.746412	-1.008333	0.608333	0.021167	0.0	1
1999-01-01	1109.397825	1109.397825	0.000000	-244.269810	148.547641	273.965461	-247.511966	694.792990	-840.360093	-0.291667	0.641667	0.098767	0.0	1
2000-01-01	2757.757519	2757.757519	0.000000	340.139894	-690.661386	-291.566666	-12.745271	367.958900	-1760.455732	0.083333	-0.066667	0.002192	0.0	1
2001-01-01	-2232.303933	0.000000	-2232.303933	56.816619	35.595123	-27.982751	-114.750162	627.934302	2681.059082	-0.700000	0.175000	-0.000308	0.0	1
2002-01-01	241.138725	241.138725	0.000000	-148.390689	181.531943	-500.759694	-150.597911	-511.790721	-435.908918	-0.241667	0.300000	0.063500	0.0	1
2003-01-01	38.507474	38.507474	0.000000	-186.762753	-218.560977	1105.700627	-97.357661	63.349341	-772.892691	0.616667	0.000000	0.021575	0.0	1
2004-01-01	730.190654	730.190654	0.000000	245.970162	-45.066727	114.727320	8.934454	673.630593	-363.256361	-0.225000	0.766667	-0.169425	0.0	1
2005-01-01	922.518162	922.518162	0.000000	170.457209	-70.989711	173.905095	-26.011829	689.483910	-532.418673	-0.525000	0.383333	-0.099592	1.0	1
2006-01-01	-886.089729	0.000000	-886.089729	173.217986	936.866393	-10.610252	-18.073730	238.566715	7.108587	-0.650000	-0.275000	-0.090092	1.0	1
2007-01-01	-584.342016	0.000000	-584.342016	268.999623	19.207126	-490.926955	-5.875584	601.592831	1382.779468	-0.483333	0.941667	-0.077108	1.0	1
2008-01-01	393.424107	393.424107	0.000000	-221.427184	-6.663868	-1268.721100	-5.623041	388.103413	1485.868417	0.108333	0.591667	-0.060192	0.0	1
2009-01-01	-1667.349199	0.000000	-1667.349199	125.550103	-315.651432	1565.111650	46.330578	-289.046007	49.623450	0.125000	0.416667	-0.007417	0.0	1
2010-01-01	446.933388	446.933388	0.000000	-463.012491	-134.196272	-310.113274	29.969873	216.193180	706.551703	2.883333	-2.383333	0.074675	0.0	1
2011-01-01	830.161197	830.161197	0.000000	61.104990	181.653671	-172.434726	2.380217	-119.755144	-1017.860060	-0.058333	-1.283333	-0.111317	0.0	1
2012-01-01	-1186.571695	0.000000	-1186.571695	267.430159	216.577571	116.087749	-0.987183	202.745156	788.234188	-1.083333	1.375000	-0.041100	0.0	1
2013-01-01	396.701645	396.701645	0.000000	143.733151	139.075529	645.385041	15.257883	311.983040	-997.654445	-0.733333	0.450000	0.010383	0.0	1
2014-01-01	-289.053915	0.000000	-289.053915	5.088233	-12.268558	-313.237415	23.739849	-796.621934	-163.410431	-0.041667	-0.366667	0.030583	0.0	1
2015-01-01	-1591.443473	0.000000	-1591.443473	-438.301999	-0.178887	-482.144162	-6.057110	-341.936691	2164.074720	0.116667	-0.533333	0.074692	0.0	1
2016-01-01	58.768905	58.768905	0.000000	-127.155353	-208.675326	-85.226565	53.886937	658.025579	1074.200854	1.316667	-0.650000	0.174125	0.0	1

mdfl_err

	program_expenditure	debt_service	corporate_income_tax	personal_income_tax	other_revenue	natural_resource_revenue	deficit	heritage_dummy	ur_lag	er_lag	cad_usd_lag
budget_dt
1964-01-01	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
1965-01-01	2327.844291	11.272854	174.729232	231.093501	1442.925275	1397.833860	-907.464724	0.0	2.500000	37.935748	NaN
1966-01-01	2891.984579	10.750872	145.136773	301.024417	1542.750138	1290.104645	-376.280521	0.0	2.500000	37.935748	NaN
1967-01-01	4436.875339	10.199713	203.994268	407.988537	2351.033944	1116.868620	367.189683	0.0	2.500000	37.935748	NaN
1968-01-01	4368.535726	19.160244	239.503055	469.425988	2639.323668	1360.377353	-320.934094	0.0	2.700000	38.322148	NaN
1969-01-01	4396.849967	17.909776	286.556413	599.977490	2444.684401	1141.748209	-58.206771	0.0	3.300000	39.041995	NaN
1970-01-01	4745.762712	38.135593	245.762712	771.186441	2737.288136	978.813559	50.847458	0.0	3.400000	39.833226	NaN
1971-01-01	4993.823780	67.916003	271.664014	767.051333	2848.477084	1090.651114	83.896240	0.0	5.200000	39.686520	NaN
1972-01-01	4988.477844	85.114978	362.663820	858.551083	2768.087112	1224.915554	-140.624746	0.0	5.700000	38.456938	1.009883
1973-01-01	5004.356719	81.151731	382.089398	977.202089	2387.213408	2160.664826	-821.661272	0.0	5.700000	39.470588	0.990792
1974-01-01	6124.378806	92.793618	829.155879	1038.689856	2352.767225	4549.880638	-2553.321174	0.0	5.300000	40.843443	1.000233
1975-01-01	7071.218716	84.149869	686.347373	925.648564	2721.722340	4417.868145	-1596.217836	0.0	3.500000	42.840909	0.978133
1976-01-01	6845.363213	59.113672	326.307469	1038.036080	2830.362613	4887.518397	-2177.747675	1.0	4.200000	43.439912	1.017267
1977-01-01	7061.151803	46.247496	554.969954	1206.639219	2720.193639	4513.335196	-1887.738708	1.0	3.891667	64.800000	0.986075
1978-01-01	6825.084687	48.260049	545.709790	1225.062794	2643.165786	4701.642511	-2242.236144	1.0	4.475000	64.633333	1.063525
1979-01-01	9302.990086	32.774318	342.491620	1265.088664	2525.261181	5181.619632	21.303307	1.0	4.750000	65.341667	1.140767
1980-01-01	9937.742745	31.376340	620.395823	1337.773062	2676.972321	4797.727697	536.250183	1.0	3.966667	67.125000	1.171558
1981-01-01	10441.551444	109.885646	701.577586	1597.568239	5094.588359	4001.769572	-844.066666	1.0	3.866667	68.050000	1.169408
1982-01-01	12281.969722	57.716023	639.073783	1731.480694	4808.269418	2887.899921	2272.961929	1.0	3.883333	69.500000	1.198892
1983-01-01	11489.190564	168.596206	771.007210	1488.773513	4813.372379	4001.941517	582.692150	1.0	7.750000	66.275000	1.233858
1984-01-01	11320.287262	218.545766	793.666203	1396.584127	5529.782999	4306.693537	-487.893837	1.0	11.008333	63.816667	1.232583
1985-01-01	12869.198063	168.831114	723.561918	1410.945740	5622.447161	3939.701880	1341.372479	1.0	11.408333	63.933333	1.295150
1986-01-01	11863.166376	263.862833	351.817111	1570.739021	4940.542816	1488.115306	3775.814955	1.0	9.775000	65.491667	1.365900
1987-01-01	10791.884860	486.136253	505.683690	1900.350807	5480.081397	2231.807343	1160.097876	0.0	10.008333	65.350000	1.389767
1988-01-01	10774.989850	655.047057	572.857965	1675.835569	5818.165763	1713.642551	1649.535059	0.0	9.525000	65.450000	1.326175
1989-01-01	10745.455671	865.692419	543.484030	1968.964999	5716.675586	1739.148895	1642.874581	0.0	7.983333	66.925000	1.230942
1990-01-01	10614.752643	923.523101	578.462597	2014.173627	5689.536231	1936.372929	1319.730359	0.0	7.158333	67.516667	1.184108
1991-01-01	10060.915107	878.291420	488.608088	2043.330951	5298.490171	1351.526066	1757.251250	0.0	6.916667	67.500000	1.167017
1992-01-01	10490.255898	920.232018	413.099221	1811.929709	5614.128666	1415.691681	2155.638638	0.0	8.250000	66.591667	1.145975
1993-01-01	9567.673764	1046.414892	540.289188	1820.154561	5604.076850	1782.195133	867.372924	0.0	9.458333	65.383333	1.208808
1994-01-01	8304.447335	1075.635389	661.029079	1886.982358	5328.892392	2081.040289	-577.861395	0.0	9.583333	64.875000	1.290167
1995-01-01	7542.256294	1000.994980	792.231321	1889.578759	4888.995090	1657.024370	-684.578266	0.0	8.783333	65.725000	1.365892
1996-01-01	7286.510699	838.743299	807.190029	1976.382124	4455.321793	2314.288966	-1427.928914	0.0	7.841667	66.650000	1.372650
1997-01-01	7598.400009	729.331650	1020.071271	2138.894710	4551.426710	2084.277589	-1466.938621	0.0	6.883333	67.316667	1.363700
1998-01-01	7647.600932	735.120709	884.383797	2452.712386	4366.478407	1262.339259	-583.192208	0.0	5.875000	67.925000	1.384867
1999-01-01	8342.393922	487.608742	640.113987	2601.260027	4640.443868	2371.737084	-1423.552301	0.0	5.583333	68.566667	1.483633
2000-01-01	8710.352822	474.863472	980.253881	1910.598641	4348.877202	5129.494603	-3184.008033	0.0	5.666667	68.500000	1.485825
2001-01-01	9338.287124	360.113309	1037.070500	1946.193764	4320.894451	2897.190669	-502.948950	0.0	4.966667	68.675000	1.485517
2002-01-01	8826.496403	209.515399	888.679810	2127.725707	3820.134757	3138.329395	-938.857868	0.0	4.725000	68.975000	1.549017
2003-01-01	8889.845744	112.157737	701.917057	1909.164731	4925.835384	3176.836868	-1711.750559	0.0	5.341667	68.975000	1.570592
2004-01-01	9563.476337	121.092191	947.887219	1864.098004	5040.562703	3907.027522	-2075.006920	0.0	5.116667	69.741667	1.401167
2005-01-01	10252.960247	95.080363	1118.344428	1793.108293	5214.467798	4829.545684	-2607.425593	1.0	4.591667	70.125000	1.301575
2006-01-01	10491.526962	77.006633	1291.562414	2729.974686	5203.857546	3943.455955	-2600.317006	1.0	3.941667	69.850000	1.211483
2007-01-01	11093.119793	71.131049	1560.562037	2749.181812	4712.930591	3359.113940	-1217.537538	1.0	3.458333	70.791667	1.134375
2008-01-01	11481.223206	65.508008	1339.134853	2742.517945	3444.209491	3752.538047	268.330878	0.0	3.566667	71.383333	1.074183
2009-01-01	11192.177199	111.838586	1464.684956	2426.866512	5009.321141	2085.188848	317.954328	0.0	3.691667	71.800000	1.066767
2010-01-01	11408.370379	141.808459	1001.672465	2292.670240	4699.207866	2532.122236	1024.506031	0.0	6.575000	69.416667	1.141442
2011-01-01	11288.615235	144.188676	1062.777455	2474.323912	4526.773140	3362.283433	6.645971	0.0	6.516667	68.133333	1.030125
2012-01-01	11491.360391	143.201492	1330.207614	2690.901483	4642.860889	2175.711738	794.880159	0.0	5.433333	69.508333	0.989025
2013-01-01	11803.343431	158.459375	1473.940765	2829.977012	5288.245930	2572.413384	-202.774285	0.0	4.700000	69.958333	0.999408
2014-01-01	11006.721496	182.199224	1479.028999	2817.708454	4975.008515	2283.359468	-366.184716	0.0	4.658333	69.591667	1.029992
2015-01-01	10664.784806	176.142114	1040.727000	2817.529567	4492.864354	691.915996	1797.890004	0.0	4.775000	69.058333	1.104683
2016-01-01	11322.810385	230.029051	913.571647	2608.854241	4407.637789	750.684901	2872.090858	0.0	6.091667	68.408333	1.278808
2017-01-01	11433.853017	319.856119	813.921696	2543.505301	5094.564399	1175.559759	2126.157981	0.0	8.133333	66.250000	1.325583
2018-01-01	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	7.883333	66.316667	1.297858

model_df_first_diff(mdfl_err)

	natural_resource_revenue	nrri	nrrd	corporate_income_tax	personal_income_tax	other_revenue	debt_service	program_expenditure	deficit	ur_lag	er_lag	cad_usd_lag	heritage_dummy	constant
budget_dt
1970-01-01	-162.934650	0.000000	-162.934650	-40.793701	171.208950	292.603734	20.225817	348.912745	109.054229	0.100000	0.791232	NaN	0.0	1
1971-01-01	111.837554	111.837554	0.000000	25.901302	-4.135108	111.188949	29.780410	248.061068	33.048782	1.800000	-0.146706	NaN	0.0	1
1972-01-01	134.264440	134.264440	0.000000	90.999806	91.499750	-80.389972	17.198975	-5.345936	-224.520986	0.500000	-1.229583	NaN	0.0	1
1973-01-01	935.749273	935.749273	0.000000	19.425579	118.651006	-380.873704	-3.963247	15.878875	-681.036526	0.000000	1.013650	-0.019092	0.0	1
1974-01-01	2389.215812	2389.215812	0.000000	447.066481	61.487767	-34.446183	11.641888	1120.022088	-1731.659902	-0.400000	1.372855	0.009442	0.0	1
1975-01-01	-132.012493	0.000000	-132.012493	-142.808507	-113.041292	368.955115	-8.643749	946.839909	957.103338	-1.800000	1.997466	-0.022100	0.0	1
1976-01-01	469.650252	469.650252	0.000000	-360.039903	112.387516	108.640274	-25.036197	-225.855503	-581.529839	0.700000	0.599003	0.039133	1.0	1
1977-01-01	-374.183202	0.000000	-374.183202	228.662485	168.603139	-110.168974	-12.866176	215.788591	290.008967	-0.308333	21.360088	-0.031192	1.0	1
1978-01-01	188.307315	188.307315	0.000000	-9.260164	18.423575	-77.027853	2.012553	-236.067116	-354.497436	0.583333	-0.166667	0.077450	1.0	1
1979-01-01	479.977121	479.977121	0.000000	-203.218170	40.025870	-117.904605	-15.485732	2477.905398	2263.539451	0.275000	0.708333	0.077242	1.0	1
1980-01-01	-383.891935	0.000000	-383.891935	277.904203	72.684398	151.711140	-1.397977	634.752660	514.946876	-0.783333	1.783333	0.030792	1.0	1
1981-01-01	-795.958126	0.000000	-795.958126	81.181763	259.795177	2417.616038	78.509306	503.808699	-1380.316848	-0.100000	0.925000	-0.002150	1.0	1
1982-01-01	-1113.869651	0.000000	-1113.869651	-62.503803	133.912455	-286.318941	-52.169623	1840.418278	3117.028595	0.016667	1.450000	0.029483	1.0	1
1983-01-01	1114.041596	1114.041596	0.000000	131.933427	-242.707181	5.102961	110.880183	-792.779158	-1690.269779	3.866667	-3.225000	0.034967	1.0	1
1984-01-01	304.752020	304.752020	0.000000	22.658992	-92.189386	716.410620	49.949560	-168.903301	-1070.585987	3.258333	-2.458333	-0.001275	1.0	1
1985-01-01	-366.991657	0.000000	-366.991657	-70.104285	14.361613	92.664162	-49.714652	1548.910801	1829.266316	0.400000	0.116667	0.062567	1.0	1
1986-01-01	-2451.586574	0.000000	-2451.586574	-371.744807	159.793281	-681.904345	95.031719	-1006.031688	2434.442476	-1.633333	1.558333	0.070750	1.0	1
1987-01-01	743.692037	743.692037	0.000000	153.866579	329.611786	539.538581	222.273420	-1071.281516	-2615.717079	0.233333	-0.141667	0.023867	0.0	1
1988-01-01	-518.164793	0.000000	-518.164793	67.174276	-224.515238	338.084366	168.910804	-16.895010	489.437183	-0.483333	0.100000	-0.063592	0.0	1
1989-01-01	25.506344	25.506344	0.000000	-29.373936	293.129430	-101.490177	210.645362	-29.534180	-6.660479	-1.541667	1.475000	-0.095233	0.0	1
1990-01-01	197.224034	197.224034	0.000000	34.978568	45.208628	-27.139354	57.830682	-130.703028	-323.144222	-0.825000	0.591667	-0.046833	0.0	1
1991-01-01	-584.846863	0.000000	-584.846863	-89.854509	29.157325	-391.046061	-45.231681	-553.837536	437.520891	-0.241667	-0.016667	-0.017092	0.0	1
1992-01-01	64.165615	64.165615	0.000000	-75.508867	-231.401242	315.638496	41.940598	429.340791	398.387388	1.333333	-0.908333	-0.021042	0.0	1
1993-01-01	366.503452	366.503452	0.000000	127.189967	8.224851	-10.051816	126.182874	-922.582134	-1288.265714	1.208333	-1.208333	0.062833	0.0	1
1994-01-01	298.845156	298.845156	0.000000	120.739891	66.827798	-275.184458	29.220498	-1263.226429	-1445.234319	0.125000	-0.508333	0.081358	0.0	1
1995-01-01	-424.015919	0.000000	-424.015919	131.202242	2.596401	-439.897302	-74.640409	-762.191041	-106.716872	-0.800000	0.850000	0.075725	0.0	1
1996-01-01	657.264596	657.264596	0.000000	14.958707	86.803365	-433.673297	-162.251681	-255.745595	-743.350647	-0.941667	0.925000	0.006758	0.0	1
1997-01-01	-230.011377	0.000000	-230.011377	212.881242	162.512585	96.104917	-109.411649	311.889310	-39.009707	-0.958333	0.666667	-0.008950	0.0	1
1998-01-01	-821.938330	0.000000	-821.938330	-135.687474	313.817676	-184.948302	5.789059	49.200923	883.746412	-1.008333	0.608333	0.021167	0.0	1
1999-01-01	1109.397825	1109.397825	0.000000	-244.269810	148.547641	273.965461	-247.511966	694.792990	-840.360093	-0.291667	0.641667	0.098767	0.0	1
2000-01-01	2757.757519	2757.757519	0.000000	340.139894	-690.661386	-291.566666	-12.745271	367.958900	-1760.455732	0.083333	-0.066667	0.002192	0.0	1
2001-01-01	-2232.303933	0.000000	-2232.303933	56.816619	35.595123	-27.982751	-114.750162	627.934302	2681.059082	-0.700000	0.175000	-0.000308	0.0	1
2002-01-01	241.138725	241.138725	0.000000	-148.390689	181.531943	-500.759694	-150.597911	-511.790721	-435.908918	-0.241667	0.300000	0.063500	0.0	1
2003-01-01	38.507474	38.507474	0.000000	-186.762753	-218.560977	1105.700627	-97.357661	63.349341	-772.892691	0.616667	0.000000	0.021575	0.0	1
2004-01-01	730.190654	730.190654	0.000000	245.970162	-45.066727	114.727320	8.934454	673.630593	-363.256361	-0.225000	0.766667	-0.169425	0.0	1
2005-01-01	922.518162	922.518162	0.000000	170.457209	-70.989711	173.905095	-26.011829	689.483910	-532.418673	-0.525000	0.383333	-0.099592	1.0	1
2006-01-01	-886.089729	0.000000	-886.089729	173.217986	936.866393	-10.610252	-18.073730	238.566715	7.108587	-0.650000	-0.275000	-0.090092	1.0	1
2007-01-01	-584.342016	0.000000	-584.342016	268.999623	19.207126	-490.926955	-5.875584	601.592831	1382.779468	-0.483333	0.941667	-0.077108	1.0	1
2008-01-01	393.424107	393.424107	0.000000	-221.427184	-6.663868	-1268.721100	-5.623041	388.103413	1485.868417	0.108333	0.591667	-0.060192	0.0	1
2009-01-01	-1667.349199	0.000000	-1667.349199	125.550103	-315.651432	1565.111650	46.330578	-289.046007	49.623450	0.125000	0.416667	-0.007417	0.0	1
2010-01-01	446.933388	446.933388	0.000000	-463.012491	-134.196272	-310.113274	29.969873	216.193180	706.551703	2.883333	-2.383333	0.074675	0.0	1
2011-01-01	830.161197	830.161197	0.000000	61.104990	181.653671	-172.434726	2.380217	-119.755144	-1017.860060	-0.058333	-1.283333	-0.111317	0.0	1
2012-01-01	-1186.571695	0.000000	-1186.571695	267.430159	216.577571	116.087749	-0.987183	202.745156	788.234188	-1.083333	1.375000	-0.041100	0.0	1
2013-01-01	396.701645	396.701645	0.000000	143.733151	139.075529	645.385041	15.257883	311.983040	-997.654445	-0.733333	0.450000	0.010383	0.0	1
2014-01-01	-289.053915	0.000000	-289.053915	5.088233	-12.268558	-313.237415	23.739849	-796.621934	-163.410431	-0.041667	-0.366667	0.030583	0.0	1
2015-01-01	-1591.443473	0.000000	-1591.443473	-438.301999	-0.178887	-482.144162	-6.057110	-341.936691	2164.074720	0.116667	-0.533333	0.074692	0.0	1
2016-01-01	58.768905	58.768905	0.000000	-127.155353	-208.675326	-85.226565	53.886937	658.025579	1074.200854	1.316667	-0.650000	0.174125	0.0	1